Question

【题目】若正项数列{}满足：，则称此数列为“比差等数列”．

（1）请写出一个“比差等数列”的前3项的值；

（2）设数列{}是一个“比差等数列”

（i）求证：；

（ii）记数列{}的前项和为，求证：对于任意，都有．

Answer 1

【答案】（1）2，4， ；（2）（i）见解析（ii）见解析

【解析】试题分析：（1）由题意可得，由迭代法，例如代入，可依次得到。（2）由，可知又，所以即，由均值不等式。由>0,可知数列{}单调递增。所以>1,

由a2≥4得，a3﹣a2≥1，a4﹣a3≥1，…，an﹣an﹣1≥1，

以上 n﹣1个不等式相加得，an≥（n﹣2）+4=n+2（n≥2），所以

当n≥2时，Sn=a1+a2+a3+…+an

≥1+4+（3+2）+…+（n+2）≥（1+2）+（2+2）+…+（n+2）﹣2

=﹣2=检验n=1也符合，即证。

试题解析：（1）解：一个“比差等数列”的前3项可以是：2，4，；

（2）（i）证明：当n=1时，，

∴===，

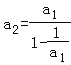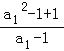∵an＞0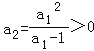，∴，则a1﹣1＞0，即a1＞1，

∴≥2+2=4，

当且仅当时取等号，

则a2≥4成立；

（ii）由an＞0得，an+1﹣an=≥0，

∴an+1≥an＞0，则an+1﹣an=，

由a2≥4得，a3﹣a2≥1，a4﹣a3≥1，…，an﹣an﹣1≥1，

以上 n﹣1个不等式相加得，an≥（n﹣2）+4=n+2（n≥2），

当n≥2时，Sn=a1+a2+a3+…+an

≥1+4+（3+2）+…+（n+2）≥（1+2）+（2+2）+…+（n+2）﹣2

=﹣2=，

当n=1时，由（i）知S1=a1＞1≥，

综上可得，对于任意n∈N*，都有Sn＞．