题目内容
14.已知矩阵A=$(\begin{array}{l}{a}&{2}\\{-1}&{4}\end{array})$.A的一个特征值λ=2.(1)求矩阵A;
(2)在平面直角坐标系中,点P(1,1)依次在矩阵A所对应的变换σ和关于x轴对称的反射变换γ的作用下得到点P′,写出复合变换γ•σ的变换公式,并求出点P′的坐标.
分析 根据矩阵M的一个特征值为1,代入特征多项式求出a的值,求出γ•σ,即可求出点P′的坐标.
解答 解:矩阵M的特征多项式f(λ)=(λ-a)(λ-4)+2,
又∵矩阵M的一个特征值为2,
∴f(2)=0,∴a=1,
由γ•σ=$[\begin{array}{l}{1}&{0}\\{0}&{-1}\end{array}][\begin{array}{l}{1}&{2}\\{-1}&{4}\end{array}]$=$[\begin{array}{l}{1}&{2}\\{1}&{-4}\end{array}]$,
设P′(x,y),则$[\begin{array}{l}{1}&{2}\\{1}&{-4}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{x}\\{y}\end{array}]$,
∴x=3,y=-3,
∴P′(3,-3).
点评 本题主要考查矩阵的特征值与变换等基础知识,考查运算求解能力及函数与方程思想,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.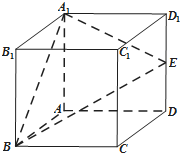 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )| A. | {2} | B. | {$\frac{{2\sqrt{5}}}{5}$} | C. | [2,2$\sqrt{2}$] | D. | [$\frac{{2\sqrt{5}}}{5}$,2] |
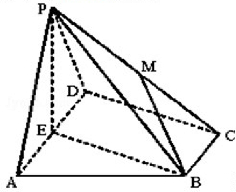 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.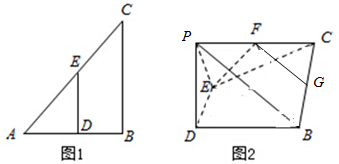
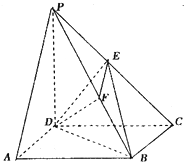 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点,作EF⊥PB交PB于点F.