题目内容
5.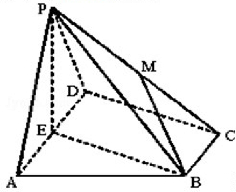 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.(1)求证:PE⊥平面ABCD;
(2)求直线BM与平面ABCD所成角的正切值.
分析 (1)根据等腰三角形得出PE⊥AD,利用面面垂直的性质可证明.
(2)建立空间坐标系,利用平面的法向量与$\overrightarrow{BM}$的夹角求解即可,sinθ=cos<$\overrightarrow{n}$,$\overrightarrow{BM}$>,转化为三角函数求解.
解答 解:(1)∵PA=PD,E为AD的中点,∴PE⊥AD.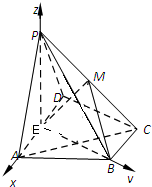
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PE⊥平面ABCD.
(2)以E为原点、EA、EB、EP分别为x轴、y轴、z轴,
建立空间直角坐标系,如图所示
则E(0,0,0),A(1,0,0),P(0,0,$\sqrt{3}$),B(0,$\sqrt{3}$,0),
M($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{BM}$=($\frac{1}{2}$,$-\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$),平面ABCD的法向量为$\overrightarrow{n}$=$\overrightarrow{EP}$=(0,0,$\sqrt{3}$),
∴$\overrightarrow{n}$$•\overrightarrow{BM}$=$\frac{3}{2}$,|$\overrightarrow{BM}$|=$\frac{\sqrt{7}}{2}$
cos<$\overrightarrow{n}$,$\overrightarrow{BM}$>=$\frac{\frac{3}{2}}{\sqrt{3}×\frac{\sqrt{7}}{2}}$=$\frac{\sqrt{21}}{7}$
设直线BM与平面ABCD所成角为θ,
sinθ=$\frac{\sqrt{21}}{7}$,cosθ=$\frac{2\sqrt{7}}{7}$,tanθ=$\frac{\sqrt{3}}{2}$
点评 本题主要考查线面关系及面面角,考查学生分析解决问题的能力,考查空间想象能力和逻辑推理能力,属于中档题

 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,D,E分别是AA1、B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,D,E分别是AA1、B1C1的中点.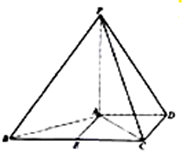 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD, 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1.