题目内容
19.如图,在Rt△ABC中,∠ABC=90°,D,E分别为AB,AC的中点,AB=4,BC=2$\sqrt{2}$,且DE为折痕,将Rt△ADE折起到图2的位置,使平面PDE⊥平面DBCE,连接PC,PB,设G是线段BC的中点,F为线段PC上的动点,满足$\overrightarrow{CF}=λ\overrightarrow{CP}$(1)当λ为何值时,平面EFG∥平面PDB,试说明理由;
(2)当λ=$\frac{1}{3}$时,求多面体PDBGFE的体积.

分析 (1)λ=$\frac{1}{2}$时,平面EFG∥平面PDB,此时F为PC的中点,证明EG∥平面PDB,FG∥平面PDB即可;
(2)利用割补法,求多面体PDBGFE的体积.
解答 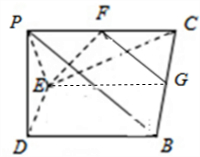 解:(1)λ=$\frac{1}{2}$时,平面EFG∥平面PDB,此时F为PC的中点.
解:(1)λ=$\frac{1}{2}$时,平面EFG∥平面PDB,此时F为PC的中点.
连接EG,则由题意,四边形DEGB是平行四边形,∴EG∥DB,
∵EG?平面PDB,DB?平面PDB
∴EG∥平面PDB,
同理FG∥PB,FG∥平面PDB,
∵EG∩FG=G,
∴平面EFG∥平面PDB;
(2)当λ=$\frac{1}{3}$时,F到平面CEG的距离为$\frac{1}{3}$PD=$\frac{2}{3}$,
∴VF-CEG=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×2×\frac{2}{3}$=$\frac{2\sqrt{2}}{9}$,
∵VP-DECB=$\frac{1}{3}×\frac{1}{2}×(\sqrt{2}+2\sqrt{2})×2×2$=2$\sqrt{2}$,
∴多面体PDBGFE的体积为2$\sqrt{2}$-$\frac{2\sqrt{2}}{9}$=$\frac{16\sqrt{2}}{9}$.
点评 本题考查图形的翻折,考查平面与平面平行的证明,考查体积的计算,正确证明线面平行是关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,分别为CD、PB的中点,AE=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,分别为CD、PB的中点,AE=$\sqrt{3}$. 在四棱锥P-ABCD中,底面ABCD为菱形,且PA⊥BD,∠BAD=60°,AB=2
在四棱锥P-ABCD中,底面ABCD为菱形,且PA⊥BD,∠BAD=60°,AB=2 如图,正四棱锥P-ABCD的顶点都在同一球面上,已知ABCD中心为E,球心O在线段PE上,QA⊥底面ABCD,且与球面交于点Q,若球的半径为2.
如图,正四棱锥P-ABCD的顶点都在同一球面上,已知ABCD中心为E,球心O在线段PE上,QA⊥底面ABCD,且与球面交于点Q,若球的半径为2. 如图,P是平面ABCD外的一点,PA⊥平面ABCD,四边形ABCD是边长为2的正方形,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q点.
如图,P是平面ABCD外的一点,PA⊥平面ABCD,四边形ABCD是边长为2的正方形,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q点.