题目内容
14.已知f(x)=$\left\{\begin{array}{l}{1-{x}^{2},x≤2}\\{f(x-1),x>2}\end{array}\right.$,那么f(4)的值是-3.分析 由分段函数的性质得到f(4)=f(3)=f(2),由此能求出结果.
解答 解:∵f(x)=$\left\{\begin{array}{l}{1-{x}^{2},x≤2}\\{f(x-1),x>2}\end{array}\right.$,
∴f(4)=f(3)=f(2)=1-22=-3.
故答案为:-3.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
相关题目
4.将指数函数f(x)的图象按向量$\overrightarrow{a}$=(1,0)平移后得到图示,则f-1(x)=( )
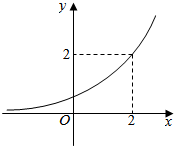

| A. | log2x | B. | 3log2x | C. | log3x | D. | 2log3x |