题目内容
8.已知f(x)为偶函数,当-1≤x≤0时,f(x)=x+1,则当0≤x≤1时,f(x)=-x+1.分析 设0≤x≤1,则-x∈[-1,0],代入可得f(-x)的解析式,进而利用偶函数的性质f(x)=f(-x)即可得出答案.
解答 解:当-1≤x≤0时,f(x)=x+1,
设0≤x≤1,则-x∈[-1,0],
又函数y=f(x)是偶函数(x∈R),
∴f(x)=f(-x)=-x+1,
∴当0≤x≤1时,f(x)=-x+1,
故答案为:-x+1.
点评 本题考查的知识点是函数的奇偶性,熟练掌握偶函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.函数y=2-x-1+1的图象可以由函数y=2-x的图象( )
| A. | 先向右平移1个单位,再向上平移1个单位得到 | |
| B. | 先向左平移1个单位,再向上平移1个单位得到 | |
| C. | 先向右平移1个单位,再向下平移1个单位得到 | |
| D. | 先向左平移1个单位,再向下平移1个单位得到 |
3.函数y=$\frac{2x}{lnx}$的图象大致为( )
| A. |  | B. | 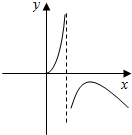 | C. | 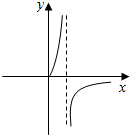 | D. | 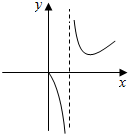 |
17.若实数x,y满足x2+y2-2x+6y+9=0,则|$\sqrt{3}$x+y-$\sqrt{3}$|的最大值、最小值分别为 ( )
| A. | 5、1 | B. | 5、0 | C. | 7、1 | D. | 7、0 |