题目内容
【题目】设函数![]() .
.
(1)若函数![]() 是R上的单调函数,求实数a的取值范围;
是R上的单调函数,求实数a的取值范围;
(2)设a=![]() ,
, ![]() (
(![]() ,
, ![]() ),
), ![]() 是
是![]() 的导函数.①若对任意的x>0,
的导函数.①若对任意的x>0, ![]() >0,求证:存在
>0,求证:存在![]() ,使
,使![]() <0;②若
<0;②若![]() ,求证:
,求证: ![]() <
<![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析: ![]() 求导得
求导得![]() ,由单调性推出a的取值范围
,由单调性推出a的取值范围![]() ①得
①得![]() ,求导,讨论
,求导,讨论![]() 和
和![]() ,代入
,代入![]() 得出结论②由函数
得出结论②由函数![]() 单调递增得
单调递增得![]() ,证得
,证得![]() ,下面证明
,下面证明![]() ,即可得证
,即可得证
解析:(1)由题意, ![]() 对
对![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 对
对![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() ,从而
,从而![]() .
.
(2)①![]() ,所以
,所以![]() .
.
若![]() ,则存在
,则存在![]() ,使
,使![]() ,不合题意,
,不合题意,
所以![]() .取
.取![]() ,则
,则![]() .
.
此时![]() .
.
所以存在![]() ,使
,使![]() .
.
②依题意,不妨设![]() ,令
,令![]() ,则
,则![]() .
.
由(1)知函数![]() 单调递增,所以
单调递增,所以![]() .
.
从而![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以![]() .
.
下面证明![]() ,即证明
,即证明![]() ,只要证明
,只要证明![]() .
.
设![]() ,所以
,所以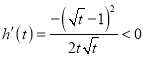 在
在![]() 恒成立.
恒成立.
所以![]() 在
在![]() 单调递减,故
单调递减,故![]() ,从而
,从而![]() 得证.
得证.
所以![]() , 即
, 即![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目