题目内容
17．已知集合A={x|x（3-x）≥0}，B={x|x≤0}，则A∩B等于（ ）| A． | 0 | B． | 0≤x≤3 | C． | {0} | D． | {x|0≤x≤3} |
分析 根据集合的基本运算进行求解即可．
解答 解：A={x|x（3-x）≥0}={x|0≤x≤3}，B={x|x≤0}，
则A∩B={0}，
故选：C．
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
如图，函数y=f（x）是可导函数，曲线y=f（x）过点（2，3），且在x=2处的切线l在y轴上的截距为2，令g（x）=xf（x），则曲线y=g（x）在x=2处的切线方程是4x-y-2=0．
3．对于函数y=f（x），当x∈（0，+∞）时，总有f（x）＜xf′（x），若m＞n＞0，则下列不等式中，恒成立的是（ ）
| A． | $\frac{f（m）}{n}$＜$\frac{f（n）}{m}$ | B． | $\frac{f（m）}{m}$＜$\frac{f（n）}{n}$ | C． | $\frac{f（m）}{n}$＞$\frac{3f（n）}{m}$ | D． | $\frac{f（m）}{m}$＞$\frac{f（n）}{n}$ |
5．甲有三本不同的书，乙去借阅，且至少借1本，则不同借法的总数为（ ）
| A． | 3 | B． | 6 | C． | 7 | D． | 9 |
12．已知函数f（x）=cos（ωx+θ）为奇函数（0＜θ＜π），其图象与直线y=1的某两个交点的横坐标分别为x1、x2，且|x2-x1|的最小值为π，则（ ）
| A． | $ω=2，θ=\frac{π}{2}$ | B． | $ω=\frac{1}{2}，θ=\frac{π}{2}$ | C． | $ω=\frac{1}{2}，θ=\frac{π}{4}$ | D． | $ω=2，θ=\frac{π}{4}$ |
9．设定义在R上的奇函数f（x）在区间（0，+∞）上单调递增，则不等式f（x-1）＜0的解集是（ ）
| A． | （-∞，1） | B． | （1，+∞） | C． | （0，+∞） | D． | （-∞，0） |
6．如图⊙O中，弦AB与弦CD相交于点P，∠B=38°，∠APD=80°，则∠A等于（ ）
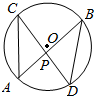
| A． | 38° | B． | 42° | C． | 80° | D． | 118° |