题目内容
6.某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为$\frac{\sqrt{5}}{2}$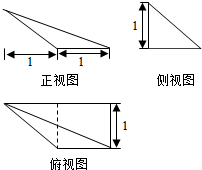
分析 由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,分别计算侧面积,即可得出结论.
解答 解:由三视图可知,几何体的直观图如图所示,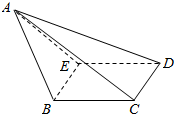
平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,
则S△AED=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
S△ABC=S△ABE=$\frac{1}{2}$×1×$\sqrt{2}$=$\frac{\sqrt{2}}{2}$,
S△ACD=$\frac{1}{2}$×1×$\sqrt{5}$=$\frac{\sqrt{5}}{2}$,
故答案为:$\frac{\sqrt{5}}{2}$
点评 本题考查三视图与几何体的关系,几何体的侧面积的求法,考查计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
8.过点(-a-6,3),(2a,3a)的直线与过点点(2,1),(3,1)的直线垂直,则实数a的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
9.点A(-3,6)关于点P(2,-1)对称点的点的坐标是( )
| A. | (1,-4) | B. | (1,4) | C. | (-7,8) | D. | (7,-8) |
11.双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的两个焦点分别为F1、F2,以F1F2为边作正△MF1F2,若双曲线恰好平分该三角形的另两边,则双曲线的离心率为( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
18.圆心在抛物线y2=2x(y>0)上,并且与抛物线的准线及x轴都相切的方程是( )
| A. | x2+y2-x-2y-$\frac{1}{4}$=0, | B. | x2+y2+x-2y+1=0, | ||
| C. | x2+y2-x+1=0, | D. | x2+y2-x-2y+$\frac{1}{4}$=0, |
15.正视图和俯视图为全等矩形的几何体不可能是( )
| A. | 四棱锥 | B. | 圆柱 | C. | 长方体 | D. | 三棱柱 |