题目内容
18.圆心在抛物线y2=2x(y>0)上,并且与抛物线的准线及x轴都相切的方程是( )| A. | x2+y2-x-2y-$\frac{1}{4}$=0, | B. | x2+y2+x-2y+1=0, | ||
| C. | x2+y2-x+1=0, | D. | x2+y2-x-2y+$\frac{1}{4}$=0, |
分析 由题意可设圆心坐标为( $\frac{{b}^{2}}{2}$,b)再跟据与抛物线的准线及x轴都相切可得 $\frac{{b}^{2}}{2}$+$\frac{1}{2}$=b 所以b=1故半径R=1可写出圆的方程为方程为(x-$\frac{1}{2}$)2+(y-1)2=1整理即可.
解答 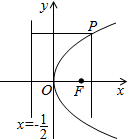 解:设圆心坐标为($\frac{{b}^{2}}{2}$,b),则由所求圆与抛物线的准线及x轴都相切可得$\frac{{b}^{2}}{2}$+$\frac{1}{2}$=b 所以b=1 故圆心为($\frac{1}{2}$,1)半径R=1 所以圆心在抛物线y2=2x(y>0)上,并与抛物线的准线及x轴都相切的圆方程为(x-$\frac{1}{2}$)2+(y-1)2=1即x2+y2-x-2y+$\frac{1}{4}$=0
解:设圆心坐标为($\frac{{b}^{2}}{2}$,b),则由所求圆与抛物线的准线及x轴都相切可得$\frac{{b}^{2}}{2}$+$\frac{1}{2}$=b 所以b=1 故圆心为($\frac{1}{2}$,1)半径R=1 所以圆心在抛物线y2=2x(y>0)上,并与抛物线的准线及x轴都相切的圆方程为(x-$\frac{1}{2}$)2+(y-1)2=1即x2+y2-x-2y+$\frac{1}{4}$=0
故选:D.
点评 此题属基础题主要考查了圆与抛物线的综合.关键是利用题中的条件求出圆心和半径结合圆的标准方程写出符合条件的方程整理即可!

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
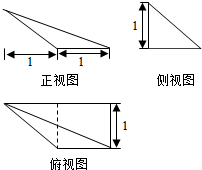



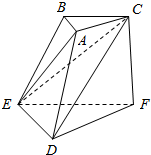 如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.