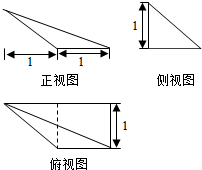
题目内容
16.已知sinθ+cosθ=$\frac{1}{5}$,双曲线x2sinθ+y2cosθ=1的焦点在y轴上,则双曲线C的离心率e=$\frac{\sqrt{21}}{3}$.分析 由同角的平方关系,结合双曲线的焦点在y轴上,可得cosθ=$\frac{4}{5}$,sinθ=-$\frac{3}{5}$,求得双曲线的标准方程,以及a,b,c,由离心率公式,计算即可得到.
解答 解:由sinθ+cosθ=$\frac{1}{5}$,sin2θ+cos2θ=1,
可得sinθ=$\frac{4}{5}$,cosθ=-$\frac{3}{5}$或cosθ=$\frac{4}{5}$,sinθ=-$\frac{3}{5}$,
由双曲线x2sinθ+y2cosθ=1的焦点在y轴上,
取cosθ=$\frac{4}{5}$,sinθ=-$\frac{3}{5}$,
可得$\frac{{y}^{2}}{\frac{5}{4}}$-$\frac{{x}^{2}}{\frac{5}{3}}$=1,
即有a2=$\frac{5}{4}$,b2=$\frac{5}{3}$,c2=$\frac{35}{12}$,
则离心率e=$\frac{c}{a}$=$\sqrt{\frac{35}{12}×\frac{4}{5}}$=$\frac{\sqrt{21}}{3}$.
故答案为:$\frac{\sqrt{21}}{3}$.
点评 本题考查双曲线的方程和性质,主要考查离心率的求法,同时考查同角的平方关系,考查运算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.某几何体的三视图如图所示(其中主视图和左视图相同),则该几何体的体积为( )
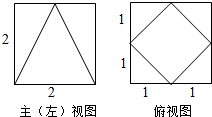

| A. | $\frac{17}{2}$ | B. | $\frac{20}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{25}{4}$ |
5.已知A、B是一锐角三角形两内角,直线l过P(1,0),以$\overrightarrow d=(sinB-cosA,cosB-sinA)$为其方向向量,则直线l一定不通过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |