题目内容
(本小题12分)在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长;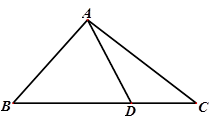
AB=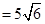 。
。
解析试题分析:先根据余弦定理求出∠ADC的值,即可得到∠ADB的值,最后根据正弦定理可得答案.
解:在△ADC中,AD=10,AC=14,DC=6,
由余弦定理得cos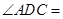
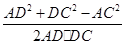 =
=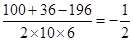 , 4分
, 4分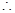
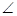 ADC="120°,"
ADC="120°," 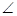 ADB=60°
ADB=60°
在△ABD中,AD="10," 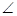 B="45°,"
B="45°," 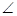 ADB=60°, 2分
ADB=60°, 2分
由正弦定理得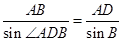 ,
, AB=
AB=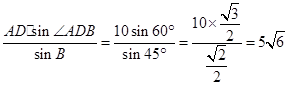 6分
6分
考点:本题主要考查余弦定理和正弦定理的应用.属基础题.
点评:解决该试题的关键是合理的选择三角形ADC,然后借助于余弦定理得到COS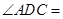 的值,再利用正弦定理得到边的求解。
的值,再利用正弦定理得到边的求解。

练习册系列答案
相关题目
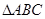 的三个内角且向量
的三个内角且向量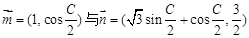 共线。
共线。 的对边分别是
的对边分别是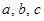 ,且满足
,且满足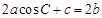 ,试判断
,试判断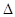
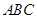 的形状.
的形状.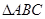 中,角
中,角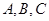 所对的边分别为
所对的边分别为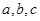 ,且满足
,且满足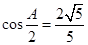 ,
,
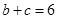 ,求
,求 的值.
的值.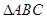 的三边长分别为
的三边长分别为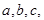 已知
已知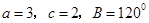 .
. 的长;(2) 求
的长;(2) 求 的面积
的面积
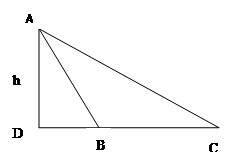
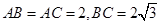 ,点D 在BC边上,∠ADC=45°。
,点D 在BC边上,∠ADC=45°。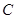 的大小;(2)求AD的长。
的大小;(2)求AD的长。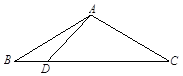
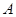 上测得正前方的河流的两岸
上测得正前方的河流的两岸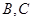 的俯角分别为
的俯角分别为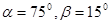 ,如果这时气球的高度
,如果这时气球的高度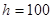 米,求河流的宽度
米,求河流的宽度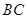 .
.
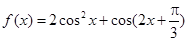
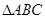 中,
中,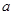 ,
,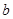 ,
, 分别是角
分别是角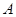 ,
,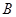 ,
,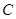 的对边;若
的对边;若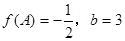 , sin(A
, sin(A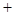 C)=
C)=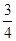 sinC,求
sinC,求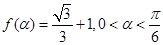 ,求
,求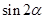 的值;
的值;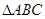 中,
中,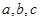 分别是角
分别是角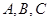 的对边,且
的对边,且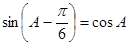 .
. 的大小;
的大小;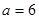 时,求
时,求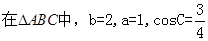 .
.