题目内容
(本题满分14分)已知函数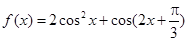
(1)在锐角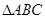 中,
中,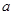 ,
,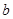 ,
, 分别是角
分别是角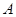 ,
,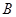 ,
,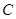 的对边;若
的对边;若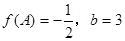 , sin(A
, sin(A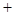 C)=
C)=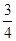 sinC,求
sinC,求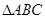 的面积.
的面积.
(2)若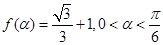 ,求
,求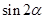 的值;
的值;
(1) 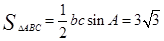 ;
;
(2)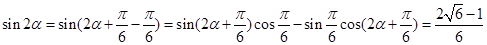 。
。
解析试题分析:(1)利用二倍角公式化简为单一三角函数,进而求解角A的值。和边b,c的值,结合正弦面积公式得到。
(2)在第一问的基础上,得到关系式,然后结凑角的思想得到函数值的求解。
解: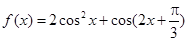
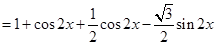

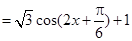 -----2分
-----2分
(1)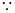
 .
.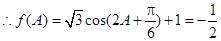 ,所以
,所以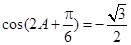 .
.
又因为 ,所以
,所以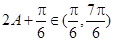 ,所以
,所以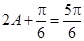 ,即
,即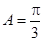 .--4分
.--4分
又因为sin(A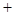 C)=
C)=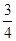 sinC,即sinB=
sinC,即sinB=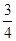 sinC,由正弦定理得
sinC,由正弦定理得 ,
,
又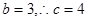 . -----6分
. -----6分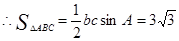 -8分
-8分
(2)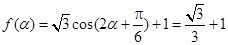 ,则
,则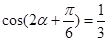
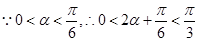 ,
,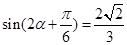 ---11分
---11分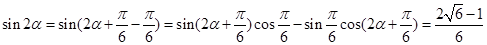 -14分
-14分
考点:本试题主要考查了三角函数的化简以及解三角形中两个定理的运用。
点评:解决该试题的关键是首先利用两角和差的关系式化为单一函数,然后借助于正弦定理和余弦定理和三角形面积公式求解得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
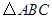 中,内角
中,内角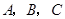 对边的边长分别是
对边的边长分别是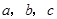 , 且
, 且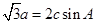
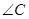
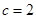 ,
, 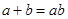 ,求ΔABC的面积
,求ΔABC的面积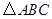 中,内角
中,内角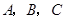 对边的边长分别是
对边的边长分别是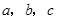 ,且
,且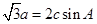
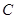 的值;
的值;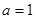 ,
,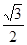
 ,求
,求 的值。
的值。
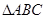 ,内角
,内角 所对的边分别为
所对的边分别为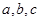 ,且满足下列三个条件:①
,且满足下列三个条件:①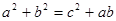 ②
②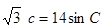 ③
③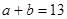
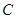 和边长
和边长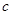 的大小; (2)
的大小; (2) 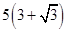 海里的两个观测点,现位于A点北偏东
海里的两个观测点,现位于A点北偏东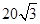 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?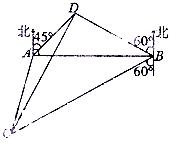
 n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东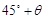 (其中
(其中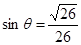 ,
,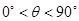 )且与点A相距10
)且与点A相距10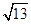 n mile的位置C.
n mile的位置C.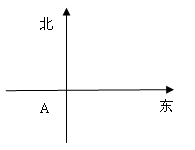
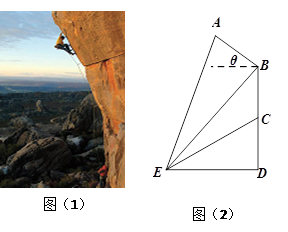
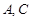 分别为两名攀岩者所在位置,点
分别为两名攀岩者所在位置,点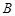 为山的拐角处,且斜坡AB的坡角为
为山的拐角处,且斜坡AB的坡角为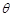 ,点
,点 为山脚,某人在地面上的点
为山脚,某人在地面上的点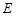 处测得
处测得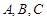 的仰角分别为
的仰角分别为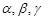 ,
,  ,
,
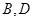 间的距离及点
间的距离及点 间的距离;
间的距离;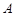 处攀岩者距地面的距离
处攀岩者距地面的距离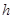 .
.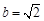 ,c=1,
,c=1,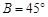 ,求A ,C, a.
,求A ,C, a.