题目内容
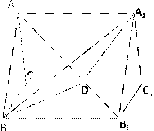
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的正弦值;
 |
解答:解法一:
(1)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() 为正三角形,
为正三角形,![]() .
.
![]() 正三棱柱
正三棱柱![]() 中,
中,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .--------------------------------------2分
.--------------------------------------2分
连结![]() ,
,
在正方形![]() 中,
中,![]() 分别为
分别为
![]() 的中点,
的中点,
![]() ,----------------------------------------------4分
,----------------------------------------------4分
![]() .在正方形
.在正方形![]() 中,
中,![]() ,
,
![]() 平面
平面![]() .----------------------------------------6分
.----------------------------------------6分
(2)设![]() 与
与![]() 交于点
交于点![]() ,在平面
,在平面![]() 中,作
中,作![]() 于
于![]() ,连结
,连结![]() ,
,
由(Ⅰ)得![]() 平面
平面![]() .
.![]() ,
,
![]() 为二面角
为二面角![]() 的平面角.----------------------8分
的平面角.----------------------8分
在![]() 中,由等面积法可求得
中,由等面积法可求得![]() ,又
,又![]() ,
,
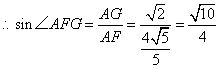 .
.
所以二面角![]() 的正弦大小
的正弦大小![]() -------------------------12分
-------------------------12分
解法二:
(1)取![]() 中点
中点![]() ,连结
,连结![]() .
.![]() 为正三角形,
为正三角形,![]() .
.
![]() 在正三棱柱
在正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .---------------------------------------2分
.---------------------------------------2分
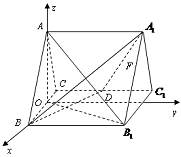
取![]() 中点
中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向
轴的正方向
建立空间直角坐标系,------------------------------------------3分
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 平面
平面![]() .------------------------------------------6分
.------------------------------------------6分
(2)设平面![]() 的法向量为
的法向量为![]()
![]() ,
,![]() .
.
 |
![]() ,
,![]() ,
,
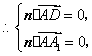
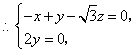
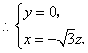
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量.--------------9分
的一个法向量.--------------9分
由(1)知![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 的法向量.
的法向量.
![]() ,
,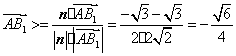 .
.
![]() 二面角
二面角![]() 的正弦大小为
的正弦大小为![]() --------------------------12分
--------------------------12分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.