题目内容
 (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)设点O为AB1上的动点,当OD∥平面ABC时,求
| AO | OB1 |
分析:(Ⅰ)由三棱柱ABC-A1B1C1为正三棱柱,取BC边的中点M,连结AM,可证AM垂直于底面,从而得到AM垂直于BD,在正方形BB1C1C中,通过直角三角形角的关系可证BD⊥B1M,利用线面垂直的判定定理得到要证的结论;
(Ⅱ)取AA1的中点为N,连结ND,OD,ON.利用线面平行的判定定理证明线面平行,从而得到面面平行,再借助于两面平行的性质得到线线平行,根据N点是AA1的中点,得到O为AB1的中点,即
=1.
(Ⅱ)取AA1的中点为N,连结ND,OD,ON.利用线面平行的判定定理证明线面平行,从而得到面面平行,再借助于两面平行的性质得到线线平行,根据N点是AA1的中点,得到O为AB1的中点,即
| AO |
| OB1 |
解答: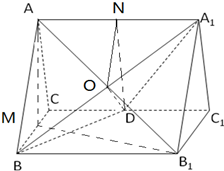 (Ⅰ)证明:取BC中点为M,连结AM,B1M,
(Ⅰ)证明:取BC中点为M,连结AM,B1M,
在正三棱柱ABC-A1B1C1中,面ABC⊥面CB1,△ABC为正三角形,
所以AM⊥BC,
故AM⊥平面CB1,又BD?平面CB1,
所以AM⊥BD.
又正方形BCC1B1中,tan∠BB1M=tan∠CBD=
,
所以∠BB1M=∠CBD,
所以BD⊥B1M,又B1M∩AM=M,
所以BD⊥平面AB1M,故AB1⊥BD,
又正方形BAA1B1中,AB1⊥A1B,A1B∩BD=B,
所以AB1⊥面A1BD;
(Ⅱ)取AA1的中点为N,连结ND,OD,ON.
因为N,D分别为AA1,CC1的中点,所以ND∥平面ABC,
又OD∥平面ABC,ND∩OD=D,所以平面NOD∥平面ABC,
所以ON∥平面ABC,又ON?平面BAA1B1,平面BAA1B1∩平面ABC=AB,
所以ON∥AB,注意到AB∥A1B1,所以ON∥A1B1,又N为AA1的中点,
所以O为AB1的中点,即
=1为所求.
 (Ⅰ)证明:取BC中点为M,连结AM,B1M,
(Ⅰ)证明:取BC中点为M,连结AM,B1M,在正三棱柱ABC-A1B1C1中,面ABC⊥面CB1,△ABC为正三角形,
所以AM⊥BC,
故AM⊥平面CB1,又BD?平面CB1,
所以AM⊥BD.
又正方形BCC1B1中,tan∠BB1M=tan∠CBD=
| 1 |
| 2 |
所以∠BB1M=∠CBD,
所以BD⊥B1M,又B1M∩AM=M,
所以BD⊥平面AB1M,故AB1⊥BD,
又正方形BAA1B1中,AB1⊥A1B,A1B∩BD=B,
所以AB1⊥面A1BD;
(Ⅱ)取AA1的中点为N,连结ND,OD,ON.
因为N,D分别为AA1,CC1的中点,所以ND∥平面ABC,
又OD∥平面ABC,ND∩OD=D,所以平面NOD∥平面ABC,
所以ON∥平面ABC,又ON?平面BAA1B1,平面BAA1B1∩平面ABC=AB,
所以ON∥AB,注意到AB∥A1B1,所以ON∥A1B1,又N为AA1的中点,
所以O为AB1的中点,即
| AO |
| OB1 |
点评:本题考查了直线与平面垂直的判定,考查了直线与平面平行的判定,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力,是中档题.

练习册系列答案
相关题目
 (2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f'(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )
(2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f'(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )