Question

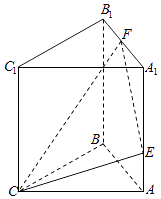
【题目】已知正三棱锥P﹣ABC的外接球的球心O满足 =0，则二面角A﹣PB﹣C的正弦值为（ ）
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：∵正三棱锥P﹣ABC的外接球的球心O满足 = ， ∴O是△ABC的外心．
设△ABC的边长为a，则此三棱锥的高PO=OB= a，
∴侧棱长PA=PB=PC= a，
侧面的斜高PD= = ，
取AC中点F，连结BF，PF，则BF⊥AC，PF⊥AC，
∵BF∩AF=F，∴AC⊥平面PBF，∵PB平面PBF，∴AC⊥PB，
作CE⊥PB，交PB于E，连结AE，∵AC∩CE=C，∴PB⊥平面ACE，
∵AE平面ACE，∴PB⊥AE，
∴∠AEC是二面角A﹣PB﹣C的平面角，
在△PBC中，由PBCE=PDBC，得CE= a，
∴cos∠AEC= = ，∴sin ，
∴二面角A﹣PB﹣C的正弦值为： ．
故选：C．