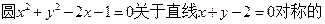题目内容
在平面直角坐标系 中,已知以O为圆心的圆与直线
中,已知以O为圆心的圆与直线 恒有公共点,且要求使圆O的面积最小.
恒有公共点,且要求使圆O的面积最小.
(1)写出圆O的方程;
(2)圆O与x轴相交于A、B两点,圆内动点P使 、
、 、
、 成等比数列,求
成等比数列,求 的范围;
的范围;
(3)已知定点Q(?4,3), 直线
直线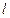 与圆O交于M、N两点,试判断
与圆O交于M、N两点,试判断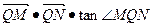 是否有最大值,若存在求出最大值,并求出此时直线
是否有最大值,若存在求出最大值,并求出此时直线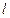 的方程,若不存在,给出理由.
的方程,若不存在,给出理由.
 中,已知以O为圆心的圆与直线
中,已知以O为圆心的圆与直线 恒有公共点,且要求使圆O的面积最小.
恒有公共点,且要求使圆O的面积最小.(1)写出圆O的方程;
(2)圆O与x轴相交于A、B两点,圆内动点P使
 、
、 、
、 成等比数列,求
成等比数列,求 的范围;
的范围;(3)已知定点Q(?4,3),
 直线
直线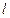 与圆O交于M、N两点,试判断
与圆O交于M、N两点,试判断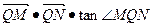 是否有最大值,若存在求出最大值,并求出此时直线
是否有最大值,若存在求出最大值,并求出此时直线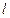 的方程,若不存在,给出理由.
的方程,若不存在,给出理由.(1)因为直线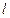 :
: 过定点T(4,3) ,由题意,要使圆
过定点T(4,3) ,由题意,要使圆 的面积最小, 定点T(4,3)在圆上, 所以圆
的面积最小, 定点T(4,3)在圆上, 所以圆 的方程为
的方程为 .
.
( 2)A(-5,0),B(5,0),设
2)A(-5,0),B(5,0),设 ,则
,则 ……①
……① 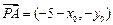 ,
,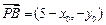 ,由
,由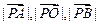 成等比数列得,
成等比数列得,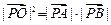 ,
,
即 ,整理得:
,整理得: ,即
,即 …② 由①②得:
…② 由①②得: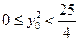 ,
,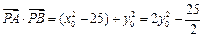 ,
,
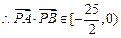
(3)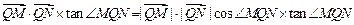
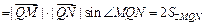
 12’
12’
由题意,得直线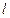 与圆O的一个交点为M(4,3),又知定点Q(
与圆O的一个交点为M(4,3),又知定点Q(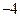 ,3),
,3),
直线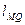 :
: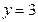 ,
,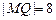 ,则当
,则当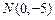 时
时 有最大值32. 14
有最大值32. 14 ’
’
即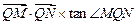 有最大值为64,此时直线
有最大值为64,此时直线 的方程为
的方程为 .
.
 :
: 过定点T(4,3) ,由题意,要使圆
过定点T(4,3) ,由题意,要使圆 的面积最小, 定点T(4,3)在圆上, 所以圆
的面积最小, 定点T(4,3)在圆上, 所以圆 的方程为
的方程为 .
. (
 2)A(-5,0),B(5,0),设
2)A(-5,0),B(5,0),设 ,则
,则 ……①
……① 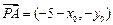 ,
,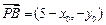 ,由
,由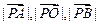 成等比数列得,
成等比数列得,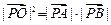 ,
,即
 ,整理得:
,整理得: ,即
,即 …② 由①②得:
…② 由①②得: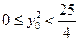 ,
,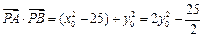 ,
,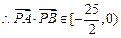
(3)
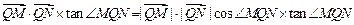
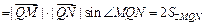
 12’
12’由题意,得直线
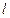 与圆O的一个交点为M(4,3),又知定点Q(
与圆O的一个交点为M(4,3),又知定点Q(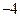 ,3),
,3),直线
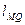 :
: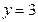 ,
,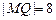 ,则当
,则当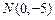 时
时 有最大值32. 14
有最大值32. 14 ’
’即
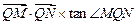 有最大值为64,此时直线
有最大值为64,此时直线 的方程为
的方程为 .
. 略

练习册系列答案
相关题目
 ,半径小于5.
,半径小于5.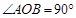 ,求直线l的方程.
,求直线l的方程.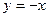 上且过两点(2,0),(0,-4)
上且过两点(2,0),(0,-4)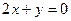 上,且与直线
上,且与直线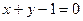 切于点(2,-1)
切于点(2,-1)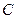 以
以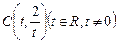 为圆心且经过原点O,与
为圆心且经过原点O,与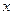 轴交于另一点A,与
轴交于另一点A,与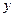 轴交于另一点B.
轴交于另一点B.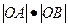 为定值
为定值 与圆
与圆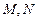 ,若
,若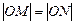 ,求圆
,求圆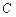 的方程.
的方程.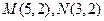 且圆心在直线
且圆心在直线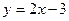 上的圆的方程
上的圆的方程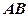 是⊙
是⊙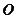 的直径,
的直径,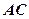 是弦,∠BAC的平分线
是弦,∠BAC的平分线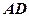 交⊙
交⊙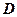 ,
,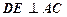 交
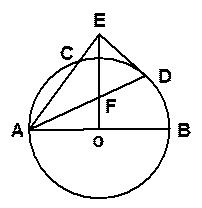
交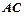 延长线于点
延长线于点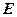 ,
,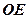 交
交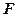 .
.
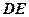 是⊙
是⊙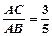 ,求
,求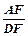 的值.
的值.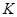 ,直线
,直线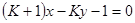 与圆
与圆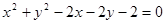 的位置关系是 ( )
的位置关系是 ( )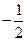 的直线
的直线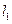 与直线
与直线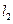 :2x + 3y -1=0交于
:2x + 3y -1=0交于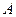 点,求过点
点,求过点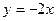 上,并与直线
上,并与直线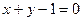 相切的圆的方程。
相切的圆的方程。