题目内容
(本小题满分12分)
求下列各圆的标准方程:
(1)圆心在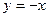 上且过两点(2,0),(0,-4)
上且过两点(2,0),(0,-4)
(2)圆心在直线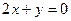 上,且与直线
上,且与直线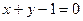 切于点(2,-1)
切于点(2,-1)
求下列各圆的标准方程:
(1)圆心在
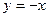 上且过两点(2,0),(0,-4)
上且过两点(2,0),(0,-4)(2)圆心在直线
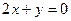 上,且与直线
上,且与直线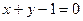 切于点(2,-1)
切于点(2,-1)解:(1)设圆心坐标为(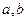 ),则所求圆的方程为
),则所求圆的方程为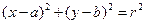 ,∵圆心在
,∵圆心在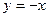 上,∴
上,∴ , ① 又∵圆过(2,0),(0,-4)∴
, ① 又∵圆过(2,0),(0,-4)∴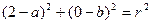 , ②
, ②
 , ③ 由①②③联立方程组,可得
, ③ 由①②③联立方程组,可得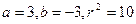
∴所求圆的方程为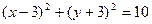

(2)∵圆与直线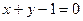 相切,并切于点M(2,-1),则圆心必在过点M(2,-1)且垂直于
相切,并切于点M(2,-1),则圆心必在过点M(2,-1)且垂直于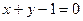 的直线
的直线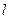 :
: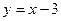 上,
上,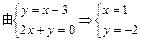 ,即圆心为C(1,-2),
,即圆心为C(1,-2),
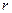 =
=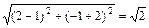 ,∴所求圆的方程为:
,∴所求圆的方程为: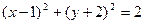

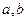 ),则所求圆的方程为
),则所求圆的方程为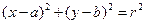 ,∵圆心在
,∵圆心在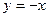 上,∴
上,∴ , ① 又∵圆过(2,0),(0,-4)∴
, ① 又∵圆过(2,0),(0,-4)∴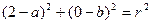 , ②
, ② , ③ 由①②③联立方程组,可得
, ③ 由①②③联立方程组,可得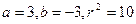
∴所求圆的方程为
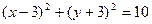

(2)∵圆与直线
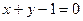 相切,并切于点M(2,-1),则圆心必在过点M(2,-1)且垂直于
相切,并切于点M(2,-1),则圆心必在过点M(2,-1)且垂直于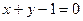 的直线
的直线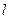 :
: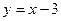 上,
上,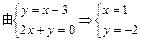 ,即圆心为C(1,-2),
,即圆心为C(1,-2),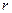 =
=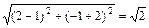 ,∴所求圆的方程为:
,∴所求圆的方程为: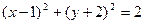

略

练习册系列答案
相关题目
 +y
+y


 经过点
经过点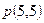 ,且与圆
,且与圆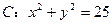 相交与
相交与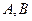 两点,截得的弦长为
两点,截得的弦长为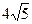 ,求
,求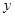 轴上,且过点
轴上,且过点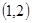 的圆的方程为( )
的圆的方程为( )

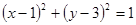

 中,已知以O为圆心的圆与直线
中,已知以O为圆心的圆与直线 恒有公共点,且要求使圆O的面积最小.
恒有公共点,且要求使圆O的面积最小. 、
、 、
、 成等比数列,求
成等比数列,求 的范围;
的范围; 直线
直线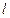 与圆O交于M、N两点,试判断
与圆O交于M、N两点,试判断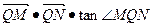 是否有最大值,若存在求出最大值,并求出此时直线
是否有最大值,若存在求出最大值,并求出此时直线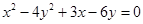 表示的图形是( )
表示的图形是( )  ,那么下列直线中经过圆心的直线方程为( )
,那么下列直线中经过圆心的直线方程为( )


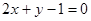
 与两坐标轴都相切,圆心
与两坐标轴都相切,圆心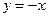 的距离等于
的距离等于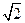 .
.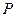 是圆
是圆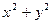 的取值范围.
的取值范围.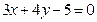 与圆C1:
与圆C1: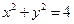 交于A,B两点,若圆C2的圆心在线段AB上,且圆C2与圆C1相切,切点在圆C1的劣弧
交于A,B两点,若圆C2的圆心在线段AB上,且圆C2与圆C1相切,切点在圆C1的劣弧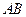 上,则圆C2的半径的最大值是 ;
上,则圆C2的半径的最大值是 ;