题目内容
对任意实数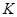
,直线
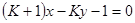与圆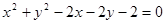
的位置关系是 ( )
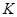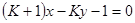,直线与圆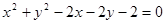的位置关系是 ( )| A．相交 | B．相切 | C．相离 | D．与K的值有关 |
A
分析：将（K+1）x-Ky-1=0转化为：K（x-y）+x-1=0，从而直线过定点（1，1），再由12+12-2×1-2×1-2＜0知点（1，1）在圆的内部得到结论．
解答：解：∵（K+1）x-Ky-1=0可化为：K（x-y）+x-1=0
∴过定点（1，1）
而12+12-2×1-2×1-2＜0
∴点（1，1）在圆的内部
∴直线与圆相交
故选A
解答：解：∵（K+1）x-Ky-1=0可化为：K（x-y）+x-1=0
∴过定点（1，1）
而12+12-2×1-2×1-2＜0
∴点（1，1）在圆的内部
∴直线与圆相交
故选A
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
中，已知以O为圆心的圆与直线
恒有公共点，且要求使圆O的面积最小.
、
、
成等比数列，求
的范围；
直线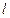
与圆O交于M、N两点，试判断
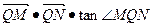是否有最大值，若存在求出最大值，并求出此时直线
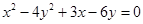表示的图形是（ ） 
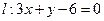和圆心为C的圆
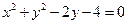相交于A、B两点，则线段AB的长度等于 
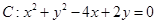关于直线
对称的圆的方程是 （ ）
，那么下列直线中经过圆心的直线方程为( )
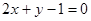
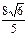，则圆的方程为（ ）
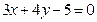与圆C1：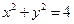
交于A,B两点，若圆C2的圆心在线段AB上，且圆C2与圆C1相切，切点在圆C1的劣弧
上，则圆C2的半径的最大值是 ；
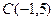为圆心，且与
轴相切的圆的方程为 ▲ ．