题目内容
(本小题满分13分)
已知二次函数 同时满足:①不等式
同时满足:①不等式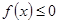 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在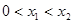 ,使得不等式
,使得不等式 成立.
成立.
设数列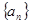 的前
的前 项和
项和 ,
,
(1)求数列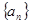 的通项公式;
的通项公式;
(2)数列 中,令
中,令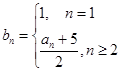 ,
,
 ,求
,求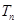 ;
;
(3)设各项均不为零的数列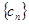 中,所有满足
中,所有满足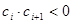 的正整数
的正整数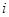 的个数称为这个数列
的个数称为这个数列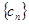 的变号数。令
的变号数。令 (
( 为正整数),求数列
为正整数),求数列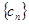 的变号数.
的变号数.
(1)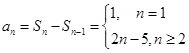 ;
;
(2) ;
;
(3)数列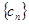 共有
共有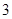 个变号数,即变号数为
个变号数,即变号数为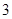 。
。
解析试题分析:(1)∵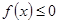 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴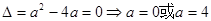 ,
,
当 时,函数
时,函数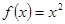 在
在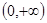 上高考资源网递增,故不存在
上高考资源网递增,故不存在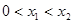 ,使得不等式
,使得不等式 成立----------------2分
成立----------------2分
当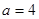 时,函数
时,函数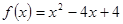 在
在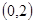 上高考资源网递减,故存在
上高考资源网递减,故存在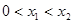 ,使得不等式
,使得不等式 成立。
成立。
综上高考资源网,得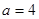 ,
,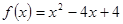 ,∴
,∴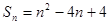 ,
,
∴ 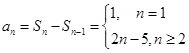 ---------------4分
---------------4分
(2)∵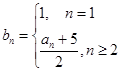 ∴
∴ 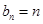
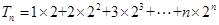
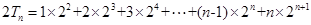
∴  --------------------8分
--------------------8分
(3)解法一:由题设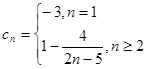 ------------9分
------------9分
∵ 时,
时,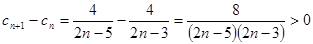 ,
,
∴ 时,数列
时,数列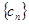 递增-------------------10分
递增-------------------10分
∵ ,由
,由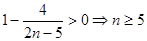 ,可知
,可知 ,即
,即 时,有且只有
时,有且只有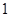 个变号数;
个变号数;
又∵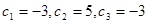 ,即
,即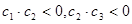 ,∴此处变号数有
,∴此处变号数有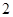 个.
个.
综上高考资源网得 数列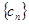 共有
共有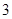 个变号数,即变号数为
个变号数,即变号数为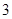 -----------13分
-----------13分
解法二:由题设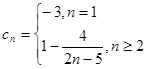 -----------(9分)
-----------(9分)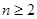 时,令
时,令 ;
;
又∵ ,∴
,∴ 时也有
时也有 .
.
综上高考资源网得:数列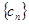 共有
共有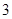 个变号数,即变号数为
个变号数,即变号数为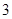 -----------13分
-----------13分
考点:本题主要考查函数的概念,等差数列、等比数列的的基础知识,“错位相消法”,简单不等式的解法。
点评:中档题,本题具有较强的综合性,本解答从处理函数问题入手,确定得到a的值,从而求得了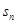 ,进一步转化成数列问题的研究。“错位相消法”是高考常常考到数列求和方法。
,进一步转化成数列问题的研究。“错位相消法”是高考常常考到数列求和方法。

练习册系列答案
相关题目
 ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 ;又知数列
;又知数列 中,
中, ,且对任意正整数
,且对任意正整数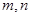 ,
, .
. 项,第
项,第 项,第
项,第 项,……,第
项,……,第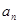 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列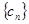 ,求数列
,求数列 项和.
项和. +
+ +…+
+…+ ] (n≥2,n∈N)
] (n≥2,n∈N) =
=
 )(1+
)(1+ )…(1+
)…(1+ )<4
)<4 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 和数列
和数列 的前n项和
的前n项和 ;
; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;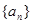 的首项为
的首项为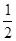 ,
,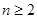 时,
时,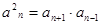 ,数列
,数列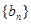 对任意
对任意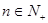 均有
均有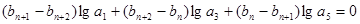
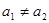 ,求证:数列
,求证:数列 ,数列
,数列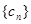 满足
满足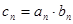 ,记数列
,记数列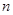 项和为
项和为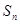 ,求证
,求证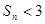 .
. 为单调递增的等差数列
为单调递增的等差数列 且
且 依次成等比数列.
依次成等比数列. ;
; 求数列
求数列 的前
的前 项和
项和 ;
; ,求证:
,求证:
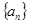 是递增数列,且满足
是递增数列,且满足 。
。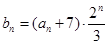 ,求数列
,求数列 的前
的前 项和
项和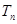 。
。 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
, .
. ,
, 为数列
为数列 的前
的前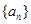 的前
的前 项和
项和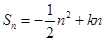 ,
,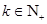 ,且
,且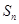 的最大值为8.
的最大值为8.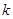 的值;
的值;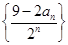 的前
的前 .
.