题目内容
(本小题满分12分)
正项数列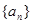 的首项为
的首项为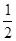 ,
,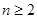 时,
时,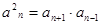 ,数列
,数列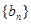 对任意
对任意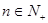 均有
均有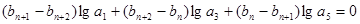
(1)若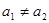 ,求证:数列
,求证:数列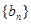 是等差数列;
是等差数列;
(2)已知 ,数列
,数列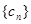 满足
满足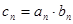 ,记数列
,记数列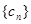 的前
的前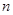 项和为
项和为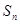 ,求证
,求证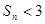 .
.
(1)利用定义法来证明即可。
(2)根据错位相减法来求和并比较大小。
解析试题分析:解:(1)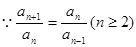 ,
, 为等比数列,设公比为
为等比数列,设公比为
又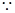
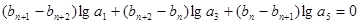



 ,即
,即
 数列
数列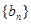 是等差数列
是等差数列
(2)





考点:考查了等差数列的概念和求和知识。
点评:对于判定数列是否为等差数列,则要考虑到相邻两项的差是否为定值,同时要利用定义的变形式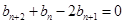 来证明结论。另外要准确并熟练的对于数列错位相减法的求和的应用属于中档题。
来证明结论。另外要准确并熟练的对于数列错位相减法的求和的应用属于中档题。

练习册系列答案
相关题目
 ,求n的值;
,求n的值; 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
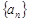 的前 n项和为
的前 n项和为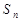 ,满足
,满足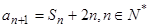 ,且
,且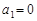 .
. ,
, ;
;  ,求证:数列
,求证:数列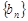 是等比数列。
是等比数列。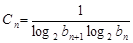 , 求数列
, 求数列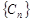 的前n项和
的前n项和 。
。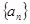 中,
中,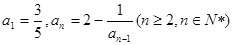 ,数列
,数列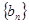 满足
满足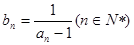 。
。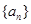 中,
中,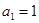 ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有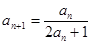 .
.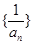 为等差数列,并求
为等差数列,并求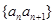 的前n项和为
的前n项和为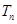 ,求使得
,求使得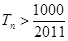 的最小正整数
的最小正整数 .
. 同时满足:①不等式
同时满足:①不等式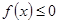 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在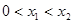 ,使得不等式
,使得不等式 成立.
成立.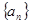 的前
的前 项和
项和 ,
, 中,令
中,令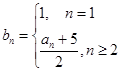 ,
,
 ,求
,求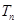 ;
;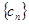 中,所有满足
中,所有满足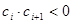 的正整数
的正整数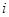 的个数称为这个数列
的个数称为这个数列 (
(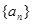 的前n项和
的前n项和 满足
满足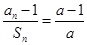 (
( >0,且
>0,且 )。数列
)。数列 满足
满足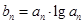
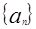 的通项。
的通项。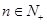 都有
都有 ,求
,求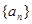 中,已知
中,已知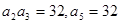 .
.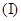 求数列
求数列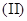 设数列
设数列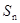 ,求
,求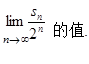
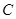 :
: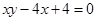 ,数列
,数列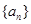 的首项
的首项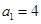 ,且当
,且当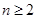 时,点
时,点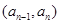 恒在曲线
恒在曲线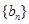 满足
满足 。
。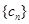 满足
满足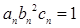 ,试比较数列
,试比较数列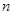 项和
项和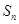 与2的大小。
与2的大小。