题目内容
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)=![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
【答案】![]()
【解析】
根据对称函数的定义,结合h(x)≥g(x)恒成立,转化为点到直线的距离d≥1,利用点到直线的距离公式进行求解即可
∵x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,
∴g(x)+h(x)=2f(x),
∵h(x)≥g(x)恒成立,
∴2f(x)=g(x)+h(x)≥g(x)+g(x)=2g(x),即f(x)≥g(x)恒成立,
作出g(x)和f(x)的图象,
则g(x)在直线f(x)的下方或重合,
则直线f(x)的截距b>0,且原点到直线y=2x+b的距离d≥1,
d=![]() b≥
b≥![]() 或
或![]() (舍去)
(舍去)
即实数b的取值范围是[![]() ,+∞),
,+∞),
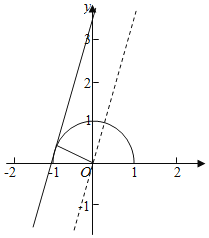
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目