题目内容
【题目】给定点
，若
是直线
上位于第一象限内的一点，直线
与
轴的正半轴相交于点
.试探究：
的面积是否具有最小值?若有，求出点的坐标；若没有，则说明理由.若点为直线
上的任意一点，情况又会怎样呢?
【答案】
的面积存在最小值为
，此时
，若
为直线
上的任意一点时，的面积不具有最小值.
【解析】
设出点
的坐标，根据
三点共线，求得参数之间的关系，将问题转化为求函数
的最小值；根据方程有根，用判别式法求得参数范围以及面积的最值.
依题意画草图如图：
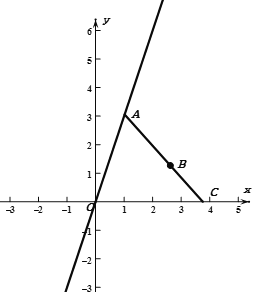
设
由
三点共线得
解得
而的面积
问题转化为求函数的最小值.
函数的定义域为
将函数式变形为
（※）
（※）方程有根
即
解得
或
（舍，
）
的面积存在最小值为，此时
若为直线上的任意一点时，的面积不具有最小值.
当无限地接近于原点
时，的面积无限地接近于
.
练习册系列答案
相关题目
