题目内容
12.设函数f(x)=3x,且f(a+2)=18,函数g(x)=3ax-4x(x∈R).(1)求g(x)的解析式;
(2)若方程g(x)-b=0在[-2,2]上有两个不同的解,求实数b的取值范围.
分析 (1)利用已知条件求出3a=2,代入g(x)=3ax-4x即可求解函数的解析式.
(2)化简方程,构造函数,利用数形结合求解实数b的取值范围.
解答 解:(1)∵函数f(x)=3x,且f(a+2)=18,∴3a+2=18⇒3a=2-----------(2分)
∵g(x)=3ax-4x=2x-4x,------------(4分)
(2)方程为2x-4x-b=0 令t=2x,x∈[-2,2],则$\frac{1}{4}≤t≤4$-----------(6分)
且方程为t-t2-b=0在有两个不同的解.
设y=t-t2=-(t-$\frac{1}{2}$)2+$\frac{1}{4}$,y=b 两函数图象在$[{\frac{1}{4},4}]$内有两个交点--------(8分)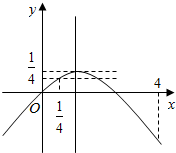
由图知$b∈[{\frac{3}{16},\frac{1}{4}})$时,方程有两不同解.--------(12分)
点评 本题考查函数的解析式的求法,函数的零点的求法,考查数形结合,考查计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.已知集合P={x|x2-2x≥0},Q={x|1<x≤2},则P∩(∁RQ)=( )
| A. | (-∞,0]∪[2,+∞) | B. | (-∞,0]∪(2,+∞) | C. | (-∞,0)∪[2,+∞) | D. | (-∞,0)∪(2,+∞) |
3.下列函数中,既为奇函数又在(0,+∞)内单调递减的是( )
| A. | f(x)=x3 | B. | f(x)=${x}^{-\frac{1}{2}}$ | C. | f(x)=-x | D. | f(x)=x+$\frac{3}{x}$ |
17.已知A={m|-1<m<0},B={m|mx2+2mx-1<0对任意实数x恒成立},则有( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
1.若向量$\vec a$,$\vec b$的夹角为$\frac{π}{3}$,且$|{\vec a}|=2$,$|{\vec b}|=1$,则向量$\vec a$与向量$\vec a-2\vec b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |