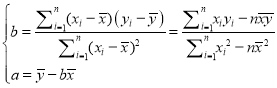题目内容
【题目】设曲线![]() 所围成的封闭区域为D.
所围成的封闭区域为D.
(1)求区域D的面积;
(2)设过点![]() 的直线与曲线C交于两点P、Q,求
的直线与曲线C交于两点P、Q,求![]() 的最大值.
的最大值.
【答案】(1)512(2)![]()
【解析】
(1)由题设,由![]() ,因此
,因此![]() .
.
若![]() ,则当
,则当![]() 时,
时,
![]()
此时![]() ,图象时两条直线段.
,图象时两条直线段.
当![]() 时,
时,
![]() ,
,![]() ,对应于一段二次函数的图象.
,对应于一段二次函数的图象.
若![]() ,则当
,则当![]() 时,类似于前面的推导得
时,类似于前面的推导得![]() ,对应于二次函数图象的一段:
,对应于二次函数图象的一段:![]() .
.
当![]() 时,
时,
![]() ,得到
,得到![]() ,无解.
,无解.
综上所述,区域D的集合为:![]() ,
,
由区域D上函数图象性质,知区域D的面积为![]() .
.
(2)设过点![]() 的直线为l,为了求
的直线为l,为了求![]() 的最大值,由区域D的对称性,只需考虑直线l与D在y轴右侧图像相交部分即可.设过点
的最大值,由区域D的对称性,只需考虑直线l与D在y轴右侧图像相交部分即可.设过点![]() 的直线l方程为
的直线l方程为![]() ,易知此时l与D相交时有
,易知此时l与D相交时有![]() .
.
1.当![]() 时,l与D分别相交于二次函数
时,l与D分别相交于二次函数![]() 以及
以及![]() ,两个交点分别为
,两个交点分别为
![]() ,
,
![]() .
.
因此,![]() ,为关于k的递减函数.
,为关于k的递减函数.
2.当![]() 时,直线l与D分别相交于二次函数
时,直线l与D分别相交于二次函数![]() 以及直线
以及直线![]() ,从图形性质容易看出,随着k从2变到1,
,从图形性质容易看出,随着k从2变到1,![]() 的值逐步减少.
的值逐步减少.
综上所述,当l经过直线![]() 与二次函数
与二次函数![]() 的图像交点
的图像交点![]() 时,
时,![]() 的值最大,此时直线l的方程为:
的值最大,此时直线l的方程为:![]() ,
,![]() ,
,![]() 的值为
的值为
![]() .
.
当![]() 落在y轴上时,
落在y轴上时,![]() .因此,
.因此,![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: