Question

【题目】关于的不等式，对于恒成立，则实数的取值范围是________.

Answer 1

【答案】

【解析】

设，则由得，则关于的不等式对任意恒成立等价于关于的不等式对任意恒成立.分别讨论当，当和当的情况下一元二次不等式的恒成立问题，依次求出t的范围最后再求并集即可.

设，则由得，

则关于的不等式对任意恒成立等价于关于的不等式对任意恒成立.

当时，不等式为，即①，

令，要使①对任意恒成立，

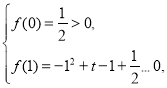则有解得；

当时，不等式为，即②，

令，对称轴，且开口向上，

则在上单调递增，要使②对任意恒成立，

则有，解得，所以；

当时，设，

易得当时，取得最小值，

则由不等式对任意恒成立得，

所以.

综上所述，的取值范围为.

故答案为：

【点晴】

本题考查不等式恒成立问题、二次函数的性质.含绝对值的不等式恒成立问题的常用解法：（1）对参数的取值范围分类讨论，去掉绝对值符号；（2）将不等式恒成立问题转化为函数的最值问题求解.