题目内容
 选修4-1:几何证明选讲
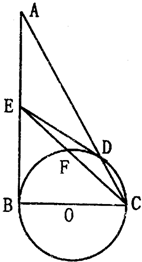
选修4-1:几何证明选讲如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(1)求证:直线DE为圆O的切线;
(2)设CE交圆O于点F,求证:CD•CA=CF•CE.
分析:(1)连接BD,OD,OE,利用BC是⊙O的直径,可得∠BDC=∠BDA=90°,利用直径三角形的斜边中线的性质可得DE=
AB=BE,于是得到OD2+DE2=OB2+BE2=OE2,利用勾股定理的逆定理可得∠ODE=90°.再利用切线的判定定理即可证明直线DE为圆O的切线;
(2)连接BF,利用BC为⊙O的直径,可得BF⊥CE;在RT△BCE中,利用射影定理可得CF•CE=BC2;同理在RT△ABC中,CD•CA=BC2,即可证明.
| 1 |
| 2 |
(2)连接BF,利用BC为⊙O的直径,可得BF⊥CE;在RT△BCE中,利用射影定理可得CF•CE=BC2;同理在RT△ABC中,CD•CA=BC2,即可证明.
解答:证明:(1)连接BD,OD,OE,则∠BDC=∠BDA=90°,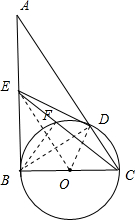
∵E为AB的中点,∴DE=
AB=BE,
∴OD2+DE2=OB2+BE2=OE2,∴∠ODE=90°.
∴直线DE为圆O的切线;
(2)连接BF,∵BC为⊙O的直径,∴BF⊥CE,
∴在RT△BCE中,CF•CE=BC2,
同理在RT△ABC中,CD•CA=BC2,
∴CD•CA=CF•CB.

∵E为AB的中点,∴DE=
| 1 |
| 2 |
∴OD2+DE2=OB2+BE2=OE2,∴∠ODE=90°.
∴直线DE为圆O的切线;
(2)连接BF,∵BC为⊙O的直径,∴BF⊥CE,
∴在RT△BCE中,CF•CE=BC2,
同理在RT△ABC中,CD•CA=BC2,
∴CD•CA=CF•CB.
点评:熟练掌握圆的性质、切线的判定定理、直角三角形斜边上中线的性质、射影定理、勾股定理的逆定理等是解题的关键.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲