题目内容
已知点
在抛物线
上，那么点到点
（2，－1）的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为（ ）
A． | B． | C． | D． |
A
解析试题分析：已知（2，－1）在抛物线内部，而抛物线上的点到焦点的距离等于到准线的距离，所以点到点（2，－1）的距离与点到抛物线焦点距离之和的最小值为点到准线的距离，而抛物线的准线为
，所以点的纵坐标为-1，代入抛物线方程知点P的坐标为.
考点：本小题主要考查抛物线的简单性质.
点评：抛物线上的点最重要的一条性质就是抛物线上的点到焦点的距离等于到准线的距离，所以在求解最值时经常利用这条性质进行转化.
练习册系列答案
相关题目
到两互相垂直的异面直线的距离相等的点，在过其中一条直线且平行于另一条直线的平面内的轨迹是（ ）。
| A．直线 | B．椭圆 | C．抛物线 | D．双曲线 |
右支上一点，
分别为双曲线的左、右焦点，I为△
的内心，若
成立，则
的值为（ ）
椭圆
和双曲线
的公共焦点为
,
是两曲线的一个交点，那么
的值是（ ）
A． | B． | C． | D． |
设已知椭圆
＋
＝1(a>b>0)的一个焦点是圆x2＋y2－6x＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为( )
| A．(－3，0) | B．(－4，0) | C．(－10，0) | D．(－5，0) |
(a＞b＞0)的两个焦点，过F2作椭圆的弦AB，若△AF1B的周长为16，椭圆的离心率
，则椭圆的方程为（ ）
双曲线
的渐近线方程为
A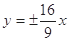． | B． | C． | D． |
已知
是椭圆
的两个焦点，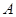
为椭圆上的一点，且
，则
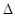
的面积是（ ）
| A．7 | B． | C． | D． |
已知双曲线
的两个焦点为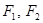
，
为坐标原点，点
在双曲线上，且
，若
、
、
成等比数列，则
等于
A． | B． | C． | D． |