题目内容
如图,三棱锥P﹣ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB.
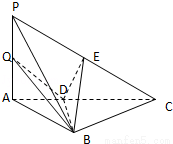
(1)求证:PC⊥平面BDE;
(2)若点Q是线段PA上任一点,判断BD、DQ的位置关系,并证明结论;
(3)若AB=2,求三棱锥B﹣CED的体积.
【答案】
(1)根据线面垂直的判定定理来加以证明,关键是对于DE⊥PC的证明的运用。
(2)点Q是线段PA上任一点都有BD⊥DQ
(3)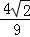 .
.
【解析】
试题分析:解:
(1)证明:由等腰三角形PBC,得BE⊥PC,又DE垂直平分PC,
∴DE⊥PC,且DE∩BE=E, ∴PC⊥平面BDE; 4分
(2)由(Ⅰ)PC⊥平面BDE,BD?平面BDE,∴PC⊥BD
同理,∵PA⊥底面ABC,∴PA⊥BD, 6分
又PA∩PC=P, ∴BD⊥面APC,DQ?面APC, ∴BD⊥DQ.
所以点Q是线段PA上任一点都有BD⊥DQ 8分
(3)∵PA=AB=2,∴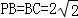 , ∵AB⊥BC,
, ∵AB⊥BC,
∴S△ABC=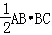 =2
=2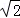 .AC=2
.AC=2
∴CD= =
=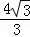 , 9分
, 9分
即S△DCB=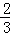 S△ABC,又E是PC的中点
S△ABC,又E是PC的中点
∴V B﹣CED=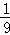 S△ABC?PA=
S△ABC?PA=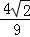 . 12分
. 12分
考点:几何体的体积,以及线面垂直
点评:解决的关键是熟练的运用空间中线面的垂直以及线线的垂直的判定定理和性质定理来证明,并利用体积公式求解,属于中档题。

练习册系列答案
相关题目
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中, (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,