题目内容
 (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中,| PA |
| AB |
| PA |
| AC |
| AB |
| AC |
| PA |
| AC |
| AB |
(Ⅰ)求证:AB⊥平面PAC;
(Ⅱ)若M为线段PC上的点,设
|
| ||
|
(Ⅲ)求二面角C-PB-A的大小.
分析:(I)根据向量垂直的充要条件可得PA⊥AB,AB⊥AC,进而由线面垂直的判定定理可得AB⊥平面PAC;
(Ⅱ)方法一:由(I)知PC⊥AB,由等腰三角形三线合一得AM⊥PC,进而由线面垂直的判定定理可得当M为PC中点时,即λ=
时,直线PC⊥平面MAB
方法二:以A为坐标原点,AC,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量垂直的充要条件及线面垂直的判定定理可得当M为PC中点时,即λ=
时,直线PC⊥平面MAB
(III)方法一:过A作AF⊥MB于F,过F作FE⊥PB于E,连结AE,由三垂线定理可知,∠AEF为二面角C-PB-A的平面角.解三角形可得答案;
方法二:求出平面BAP法向量和平面PBC的法向量.代入向量夹角公式,可得答案.
(Ⅱ)方法一:由(I)知PC⊥AB,由等腰三角形三线合一得AM⊥PC,进而由线面垂直的判定定理可得当M为PC中点时,即λ=
| 1 |
| 2 |
方法二:以A为坐标原点,AC,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量垂直的充要条件及线面垂直的判定定理可得当M为PC中点时,即λ=
| 1 |
| 2 |
(III)方法一:过A作AF⊥MB于F,过F作FE⊥PB于E,连结AE,由三垂线定理可知,∠AEF为二面角C-PB-A的平面角.解三角形可得答案;
方法二:求出平面BAP法向量和平面PBC的法向量.代入向量夹角公式,可得答案.
解答:证明: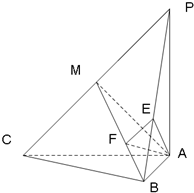 (Ⅰ)∵
(Ⅰ)∵
•
=
•
=
•
=0,
∴PA⊥AB,AB⊥AC,
∵PA∩AC=A,PA,AC?平面PAC
∴AB⊥平面PAC. …(3分)
方法一:(Ⅱ)当M为PC中点时,即λ=
时,直线PC⊥平面MAB,…(4分)
证明如下:
由(Ⅰ)知AB⊥平面PAC,PC?平面APC,
∴PC⊥AB,…(5分)
在等腰△CAP中,
∵M为PC中点,
∴AM⊥PC,…(6分)
又∵BA∩AM=A,BA,AM?平面MAB
∴PC⊥平面MAB. …(8分)
(Ⅲ)由(Ⅱ)知当M为PC中点时,PC⊥平面MAB,
∵PC?平面PBC,
∴平面PCB⊥平面MAB. …(9分)
过A作AF⊥MB于F,
∴AF⊥平面PBC
作FE⊥PB于E,连结AE,由三垂线定理可知,AE⊥PB.
∴∠AEF为二面角C-PB-A的平面角. …(11分)
设AB=a,则AC=AP=2a.
在Rt△PAC中,AM=
a,
由(Ⅰ)知AB⊥平面PAC,AM?平面APC,
∴AB⊥AM.
在Rt△BAM中,BM2=AB2+AM2⇒BM=
=
a.
由面积公式得BM•AF=AB•AM,AF=
a,…(12分)
同理,在Rt△BAP中,BP=
a,由面积公式得AE=
a,…(13分)
在Rt△AFE中,sin∠AEF=
=
.
所以二面角C-PB-A的大小为arcsin
. …(14分)
方法二:
(Ⅰ)同方法一. …(3分)
(Ⅱ)如图,以A为坐标原点,AC,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
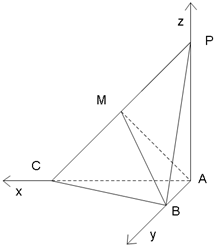
设AP=2,则P(0,0,2),A(0,0,0),C(2,0,0),B(0,1,0),…(4分)
当M为PC中点时,即λ=
时,直线PC⊥平面MAB. …(5分)
证明如下:
当M为PC中点时,M(1,0,1).
=(2,0,-2),
=(1,0,1),
=(-1,1,-1).
•
=2×1+0×0+(-2)×1=0,
∴
⊥
,即PC⊥AM. …(6分)
•
=2×(-1)+0×1+(-2)×(-1)=0,
∴
⊥
,即PC⊥BM. …(7分)
又∵AM∩BM=M,
∴PC⊥平面AMB. …(8分)
(Ⅲ)可证CA⊥平面BAP.
则平面BAP法向量为
=(2,0,0),…(9分)
下面求平面PBC的法向量.
设平面PBC的法向量为
=(x,y,z),
=(2,0,-2),
=(-2,1,0),
⇒
=(z,2z,z),
令z=1,则
=(1,2,1),…(12分)
cos<
,
>=
=
=
.
所以二面角C-PB-A的大小为arccos
. …(14分)
 (Ⅰ)∵
(Ⅰ)∵| PA |
| AB |
| PA |
| AC |
| AB |
| AC |
∴PA⊥AB,AB⊥AC,
∵PA∩AC=A,PA,AC?平面PAC
∴AB⊥平面PAC. …(3分)
方法一:(Ⅱ)当M为PC中点时,即λ=
| 1 |
| 2 |
证明如下:
由(Ⅰ)知AB⊥平面PAC,PC?平面APC,
∴PC⊥AB,…(5分)
在等腰△CAP中,
∵M为PC中点,
∴AM⊥PC,…(6分)
又∵BA∩AM=A,BA,AM?平面MAB
∴PC⊥平面MAB. …(8分)
(Ⅲ)由(Ⅱ)知当M为PC中点时,PC⊥平面MAB,
∵PC?平面PBC,
∴平面PCB⊥平面MAB. …(9分)
过A作AF⊥MB于F,
∴AF⊥平面PBC
作FE⊥PB于E,连结AE,由三垂线定理可知,AE⊥PB.
∴∠AEF为二面角C-PB-A的平面角. …(11分)
设AB=a,则AC=AP=2a.
在Rt△PAC中,AM=
| 2 |
由(Ⅰ)知AB⊥平面PAC,AM?平面APC,
∴AB⊥AM.
在Rt△BAM中,BM2=AB2+AM2⇒BM=
| a2+2a2 |
| 3 |
由面积公式得BM•AF=AB•AM,AF=
| ||
|
同理,在Rt△BAP中,BP=
| 5 |
| 2 | ||
|
在Rt△AFE中,sin∠AEF=
| AF |
| AE |
| ||
| 6 |
所以二面角C-PB-A的大小为arcsin
| ||
| 6 |
方法二:
(Ⅰ)同方法一. …(3分)
(Ⅱ)如图,以A为坐标原点,AC,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系.

设AP=2,则P(0,0,2),A(0,0,0),C(2,0,0),B(0,1,0),…(4分)
当M为PC中点时,即λ=
| 1 |
| 2 |
证明如下:
当M为PC中点时,M(1,0,1).
| PC |
| AM |
| MB |
| PC |
| AM |
∴
| PC |
| AM |
| PC |
| MB |
∴
| PC |
| MB |
又∵AM∩BM=M,
∴PC⊥平面AMB. …(8分)
(Ⅲ)可证CA⊥平面BAP.
则平面BAP法向量为
| n1 |
下面求平面PBC的法向量.
设平面PBC的法向量为
| n2 |
| PC |
| CB |
|
| n2 |
令z=1,则
| n2 |
cos<
| n1 |
| n2 |
| ||||
|
| 2 | ||
2×
|
| ||
| 6 |
所以二面角C-PB-A的大小为arccos
| ||
| 6 |
点评:本题考查的知识点是用空间向量求平面间的夹角,线面垂直的证明,解法一的关键是熟练掌握线面垂直的判定定理及二面角的平面角的求法,解法二的关键是建立空间坐标系,将空间线面垂直及夹角问题转化为向量垂直和夹角问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目