题目内容
 (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2| 2 |
(Ⅰ)求证:PA⊥平面PBC;
(Ⅱ)若E为侧棱PB的中点,求直线AE与底面ABC所成角的正弦值.
分析:(Ⅰ)先证明PA⊥PC,再证明BC⊥平面ACP,可得PA⊥BC,利用线面垂直的判定,可得PA⊥平面PBC;
(Ⅱ)取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,证明∠EAH为直线AE与底面ABC所成角,且sin∠EAH=
,由此可得结论.
(Ⅱ)取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,证明∠EAH为直线AE与底面ABC所成角,且sin∠EAH=
| EH |
| AE |
解答: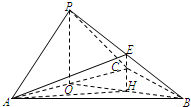 (Ⅰ) 证明:由∠APC=90°知,PA⊥PC,
(Ⅰ) 证明:由∠APC=90°知,PA⊥PC,
又AP=PC=2,所以AC=2
,…(2分)
又AB=4,BC=2
,所以AC2+BC2=AB2,
所以∠ACB=90°,即BC⊥AC,…(3分)
又侧面PAC⊥底面ABC,侧面PAC∩底面ABC平面=AC,BC?平面ABC,
所以BC⊥平面ACP,所以PA⊥BC,…(5分)
又PC∩BC=C,所以PA⊥平面PBC…(6分)
(Ⅱ)解:如图,取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,
∵BC⊥平面ACP,PO?平面ACP
∴BC⊥PO
∵AC∩BC=C,∴PO⊥平面ABC,
又E为侧棱PB的中点,H为OB中点,∴EH∥PO
∴EH⊥平面ABC,…(8分)
∴∠EAH为直线AE与底面ABC所成角,且sin∠EAH=
…(10分)
又PO=
AC=
,∴EH=
PO=
,
∵PA⊥平面PBC,PB?平面PBC,∴AP⊥PB,∴PB=2
,PE=
,
∴AE=
,…(11分)
∴sin∠EAH=
=
=
所以直线AE与底面ABC所成角的正弦值为
.…(12分)
 (Ⅰ) 证明:由∠APC=90°知,PA⊥PC,
(Ⅰ) 证明:由∠APC=90°知,PA⊥PC,又AP=PC=2,所以AC=2
| 2 |
又AB=4,BC=2
| 2 |
所以∠ACB=90°,即BC⊥AC,…(3分)
又侧面PAC⊥底面ABC,侧面PAC∩底面ABC平面=AC,BC?平面ABC,
所以BC⊥平面ACP,所以PA⊥BC,…(5分)
又PC∩BC=C,所以PA⊥平面PBC…(6分)
(Ⅱ)解:如图,取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,
∵BC⊥平面ACP,PO?平面ACP
∴BC⊥PO
∵AC∩BC=C,∴PO⊥平面ABC,
又E为侧棱PB的中点,H为OB中点,∴EH∥PO
∴EH⊥平面ABC,…(8分)
∴∠EAH为直线AE与底面ABC所成角,且sin∠EAH=
| EH |
| AE |
又PO=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵PA⊥平面PBC,PB?平面PBC,∴AP⊥PB,∴PB=2
| 3 |
| 3 |
∴AE=
| 7 |
∴sin∠EAH=
| EH |
| AE |
| ||||
|
| ||
| 14 |
所以直线AE与底面ABC所成角的正弦值为
| ||
| 14 |
点评:本题主要考查了直线与平面垂直的判定,考查线面角,掌握线面垂直的判定,正确作出线面角是关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目