题目内容
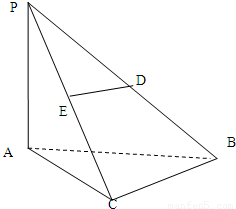
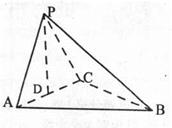
 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2| 3 |
(1)求证:AB⊥平面PAC. (2)设二面角A-PC-B•的大小为θ•,求tanθ•的值.
分析:(1)在平面PAC内找到并且证明两条相交直线分别与已知直线垂直,即可得到线面垂直.
(2)根据二面角的定义作出二面角,并且证明此角是所求角,然后结合解三角形的有关知识求解答案.
(2)根据二面角的定义作出二面角,并且证明此角是所求角,然后结合解三角形的有关知识求解答案.
解答:解:(1)在△ABC中因为AC=2,BC=4,AB=2
,
所以根据勾可得∠BAC=90°即AB⊥AC.
又因为AB⊥PC,PC∩AC=C,PC?平面ACP,AC?平面ACP,
所以AB⊥平面PAC.
(2)过点A作AD⊥PC,角PC与点D,连接BD.
因为AB⊥平面PAC,PC?平面PAC,
所以PC⊥AB.
又因为AD⊥PC,AD?平面ABD,AD?平面ABD,AD∩AB=A,
所以PC⊥平面ABD,所以PC⊥BD.
所以∠BDA是二面角A-PC-B的平面角,即∠BDA=θ.
在△ADC中,AC=2,∠ACD=30°,∠ADC=90°,所以AD=1.
在△ABD中,AB=2
,AD=1,
所以tanθ=
=2
.
| 3 |

所以根据勾可得∠BAC=90°即AB⊥AC.
又因为AB⊥PC,PC∩AC=C,PC?平面ACP,AC?平面ACP,
所以AB⊥平面PAC.
(2)过点A作AD⊥PC,角PC与点D,连接BD.
因为AB⊥平面PAC,PC?平面PAC,
所以PC⊥AB.
又因为AD⊥PC,AD?平面ABD,AD?平面ABD,AD∩AB=A,
所以PC⊥平面ABD,所以PC⊥BD.
所以∠BDA是二面角A-PC-B的平面角,即∠BDA=θ.
在△ADC中,AC=2,∠ACD=30°,∠ADC=90°,所以AD=1.
在△ABD中,AB=2
| 3 |
所以tanθ=
| AB |
| AD |
| 3 |
点评:解决此类问题的关键是熟练掌握几何体的结构特征,利用题中线面关系证明线面垂直并且有利于求解二面角的平面角.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
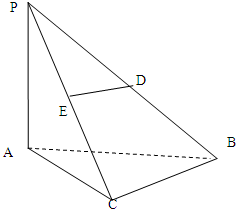 如图在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC,
如图在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC,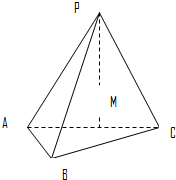 如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.
如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.
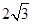 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值.