题目内容
【题目】已知椭圆![]() 的焦距与短轴长相等,长轴长为
的焦距与短轴长相等,长轴长为![]() ,设过右焦点F倾斜角为
,设过右焦点F倾斜角为![]() 的直线交椭圆M于A、B两点.
的直线交椭圆M于A、B两点.
(1)求椭圆M的方程;
(2)求证:![]()
(3)设过右焦点F且与直线AB垂直的直线交椭圆M于C、D,求四边形ABCD面积的最小值.
【答案】(1)![]() ;(2)详见解析;(3)16
;(2)详见解析;(3)16
【解析】
(1)根据条件可知![]() ,再根据
,再根据![]() ,求解方程;
,求解方程;
(2)分![]() 和
和![]() 两种情况求弦长,当
两种情况求弦长,当![]() 时,设直线
时,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,得到根与系数的关系,
,与椭圆方程联立,得到根与系数的关系,![]() ,
,![]() ,代入弦长公式
,代入弦长公式![]() ,再根据
,再根据![]() 证明;
证明;
(3)由题意可知四边形![]() 的面积是
的面积是![]() ,根据
,根据![]() ,代入弦长公式可得
,代入弦长公式可得![]() ,
,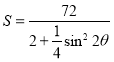 再根据三角函数求函数的最小值.
再根据三角函数求函数的最小值.
(1)由题意可知,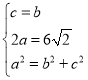 ,
,
解得:![]() ,
,
![]() 椭圆方程是:
椭圆方程是:![]() ;
;
(2)当![]() 时,
时,![]() ,此时
,此时![]() ,满足
,满足![]()
当![]() 时,设直线的斜率为
时,设直线的斜率为![]() ,
,![]()
设直线![]() 的方程为
的方程为![]() ,
,
由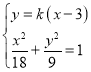 得
得
![]()
设![]()
![]() ,
,![]() ,
,
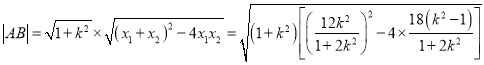
![]() ,
,
![]() ,代入上式,
,代入上式,
![]() ,
,
综上可知:![]() .
.
(3)过右焦点![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于
于![]() 两点,
两点,
![]() ,
,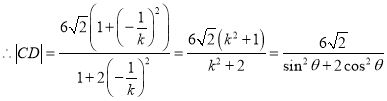 ,
,
![]() ,
,
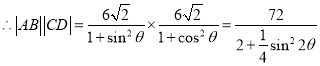 ,
,
当![]() 时,
时,![]() 的最小值是
的最小值是![]() .
.
而四边形![]() 的面积是
的面积是![]() ,
,
![]() 四边形
四边形![]() 的面积的最小值是
的面积的最小值是![]() .
.

练习册系列答案
相关题目
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
