Question

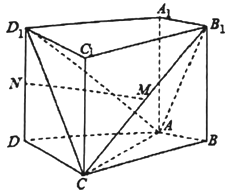
【题目】如图，在四棱柱中，侧棱底面， ， ， ， ，且点和分别为和的中点．

（1）求证： 平面；

（2）求二面角的正弦值．

Answer 1

【答案】(1)见解析(2)

【解析】试题分析：（Ⅰ）以A为原点建立空间直角坐标系，利用向量法能证明MN∥平面ABCD．
（Ⅱ）求出两个平面的法向量，可计算两个平面所成二面角的余弦值的大小，再求正弦值即可．

试题解析：

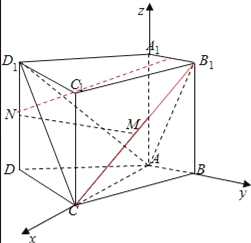
（1）证明：如图，以A为坐标原点，以AC、AB、AA1所在直线分别为x、y、z轴建系，

则A（0，0，0），B（0，1，0），C（2，0，0），D（1，﹣2，0），

A1（0，0，2），B1（0，1，2），C1（2，0，2），D1（1，﹣2，2），

又∵M、N分别为B1C、D1D的中点，∴M（1，，1），N（1，﹣2，1）．

由题可知： =（0，0，1）是平面ABCD的一个法向量， =（0，﹣，0），

∵=0，MN平面ABCD，∴MN∥平面ABCD；

（2）解：由（I）可知： =（1，﹣2，2），=（2，0，0），=（0，1，2），

设=（x，y，z）是平面ACD1的法向量，

由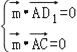，得，

取z=1，得=（0，1，1），

设=（x，y，z）是平面ACB1的法向量，

由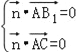，得，

取z=1，得=（0，﹣2，1），

∵cos＜，＞==﹣，∴sin＜，＞==，

∴二面角D1﹣AC﹣B1的正弦值为；