题目内容
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 有两个相异零点
有两个相异零点![]() ,
, ![]() ,求证:
,求证: ![]() .(其中e为自然对数的底数)
.(其中e为自然对数的底数)
【答案】(Ⅰ)见解析; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由题意得![]() ,分
,分![]() 和
和![]() 两种情况分类讨论,即可求解函数的单调区间;
两种情况分类讨论,即可求解函数的单调区间;
(Ⅱ)要证: ![]() ,即证
,即证![]() ,不妨设
,不妨设![]() ,∵
,∵![]() ,
, ![]() 是函数
是函数![]() 的零点, 化简
的零点, 化简![]() ,则转化为证:
,则转化为证: ![]() ,构造函数
,构造函数![]() ,利用
,利用![]() 单调性与最值,即可作出证明.
单调性与最值,即可作出证明.
试题解析:(Ⅰ) ![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
① 当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增,
上单调递增,
② 当![]() 时,令
时,令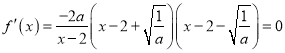 ,解得
,解得![]() ,
,
![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增,
单调递增,
![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递减,
单调递减,
综上所述,当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() 在
在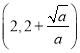 上单调递增,在
上单调递增,在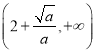 上单调递减;
上单调递减;
(Ⅱ)证法一 要证: ![]() ,则证
,则证![]() ,
,
即证![]() ,
,
不妨设![]() ,∵
,∵![]() ,
, ![]() 是函数
是函数![]() 的零点,则
的零点,则![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
则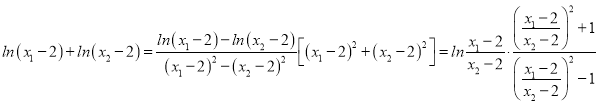 ,
,
则转化为证: ,令
,令![]() ,则
,则![]() ,
,
于是即证: ![]() ,可化为
,可化为![]() ,即证
,即证![]() ,
,
构造函数![]() ,
, ![]() ,
,
令![]() ,则
,则![]() ,则
,则![]() 在
在![]() 单增,则
单增,则![]() ,
,
则![]() ,则
,则![]() 在
在![]() 单增,则
单增,则![]() ,即
,即![]() 成立,
成立,
所以![]() 成立.
成立.
证法二 ![]() 的定义域为
的定义域为![]() ,要证:
,要证: ![]() ,则证
,则证![]() ,
,
即证![]() ,令
,令![]() ,
, ![]() ,
,
即证![]() ,也即证
,也即证![]() ,
,
因为![]() ,
, ![]() 是函数
是函数![]() 的相异零点,则
的相异零点,则![]() ,
, ![]() ,
,
所以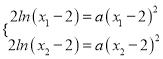 ,即
,即![]() ,所以,
,所以, 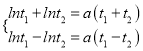 ,
,
所以 ,
,
不妨设![]() ,则
,则![]() ,令
,令![]() (
(![]() ),
),
要证![]() ,则转化为证
,则转化为证![]() (其中
(其中![]() ),即证
),即证![]() ,……10分
,……10分
令![]() (
(![]() ),则
),则![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即
,即![]() 成立,
成立,
从而原命题![]() 成立
成立
证法三 ![]() 的定义域为
的定义域为![]() ,要证:
,要证: ![]() ,则证
,则证![]() ,
,
即证![]() ,令
,令![]() ,
, ![]() ,
, ![]() ,
,
则转化为证明命题“函数![]() 有两个相异的零点
有两个相异的零点![]() ,
, ![]() ,求证
,求证![]() ”,……6分
”,……6分
∵![]() ,
,
①当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() 没有两个零点,不合题意;
没有两个零点,不合题意;
②当![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
要使![]() 有两个相异零点,则
有两个相异零点,则![]() ,解得
,解得![]() ;
;
且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
不妨设![]() ,要证
,要证![]() ,即证
,即证![]() ,
,
而![]() ,所以
,所以![]() ,
, ![]() ,
,
而函数![]() 在
在![]() 上单调递增,要证
上单调递增,要证![]() ,只要证
,只要证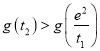 ,而
,而![]() ,即证
,即证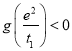 ,
,
由于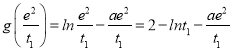 ,而
,而![]() ,即
,即![]() ,
,
∴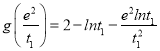 (
(![]() ),记
),记![]() (
(![]() ),
),
∴![]() ,
,
令![]() (
(![]() ),则
),则![]() ,
,
∴![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,即
,即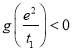 成立,
成立,
从而原命题![]() 成立 .
成立 .