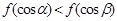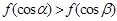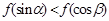题目内容
已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2,若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )
A.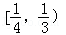 | B.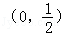 |
C.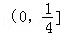 | D.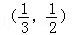 |
C
解析试题分析:根据f(x+1)=﹣f(x),可得f(x)是周期为2的周期函数. 再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,可得函数在[﹣1,3]上的解析式.根据题意可得
函数y=f(x)的图象与直线y="kx+k" 有4个交点,数形结合可得实数k的取值范围.
∵函数f(x)满足f(x+1)=﹣f(x),故有f(x+2)=f(x),故f(x)是周期为2的周期函数.再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,
可得当x∈[﹣1,0]时,f(x)=x2,故当x∈[﹣1,1]时,f(x)=x2,当x∈[1,3]时,f(x)=(x﹣2)2.
由于函数g(x)=f(x)﹣kx﹣k有4个零点,故函数y=f(x)的图象与直线y="kx+k" 有4个交点,如图所示:
把点(3,1)代入y=kx+k,可得k=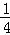 ,数形结合可得实数k的取值范围是 (0,
,数形结合可得实数k的取值范围是 (0,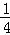 ],
],
故选C.
考点:根的存在性及根的个数判断
点评:本题主要考查函数的周期性的应用,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案设函数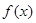 满足
满足 且当
且当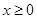 时,
时,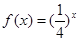 ,又函数
,又函数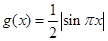 ,则函数
,则函数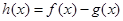 在
在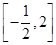 上的零点个数为 ( )
上的零点个数为 ( )
A.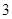 | B.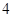 | C. | D.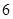 |
设函数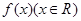 满足
满足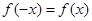 ,
,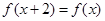 ,则函数
,则函数 的图象可以是( )
的图象可以是( )
A.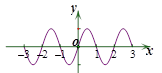 | B.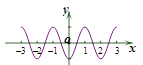 |
C.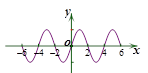 | D.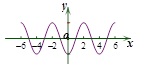 |
下列四个函数中,既是奇函数又在定义域上单调递增的是( )
A.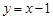 | B.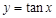 | C.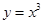 | D.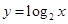 |
设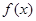 是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则
是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则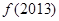 +
+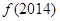 =( )
=( )
| A.3 | B.2 | C.1 | D.0 |
已知定义域在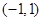 上的奇函数
上的奇函数 是减函数,且
是减函数,且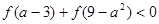 ,则
,则 的取值范围是( )
的取值范围是( )
A.(2 ,3) ,3) | B.(3, ) ) | C.(2 ,4) ,4) | D.(-2,3) |
下列函数在(0,+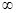 )上是增函数的是( )
)上是增函数的是( )
A.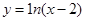 | B.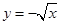 | C.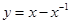 | D.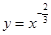 |
函数f(x)=2x-sinx的零点个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
 满足
满足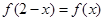 ,且在
,且在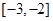 上是减函数,
上是减函数,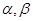 是钝角三角形的两个锐角,则下列不等式中正确的是( )
是钝角三角形的两个锐角,则下列不等式中正确的是( )