题目内容
定义在R上的偶函数 满足
满足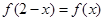 ,且在
,且在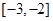 上是减函数,
上是减函数,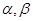 是钝角三角形的两个锐角,则下列不等式中正确的是( )
是钝角三角形的两个锐角,则下列不等式中正确的是( )
A. | B.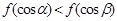 | C.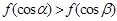 | D.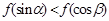 |
D
解析试题分析:∵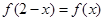 ,∴
,∴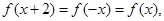 ∴T=2
∴T=2
∵ 在[-3,-2]上是减函数,∴在[-1,0]上是减函数,
在[-3,-2]上是减函数,∴在[-1,0]上是减函数,
∵函数是偶函数,∴在[0,1]上是增函数
∵α,β是钝角三角形的两个锐角,∴0<α+β<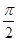
∴0<α<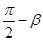 <
<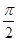 ,
,
∴0<sinα<sin(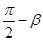 )=cosβ<1
)=cosβ<1
∴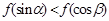 ,故选B.
,故选B.
考点:奇偶性与单调性的综合,函数的周期性.

练习册系列答案
相关题目
方程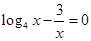 的根所在区间为( )
的根所在区间为( )
A.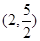 | B.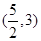 | C.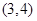 | D.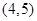 |
设函数 ,若实数
,若实数 满足
满足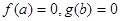 ,则( )
,则( )
A. | B. |
C. | D. |
已知函数 ,定义函数
,定义函数 给出下列命题:
给出下列命题:
① ; ②函数
; ②函数 是奇函数;③当
是奇函数;③当 时,若
时,若 ,
, ,总有
,总有 成立,其中所有正确命题的序号是( )
成立,其中所有正确命题的序号是( )
| A.② | B.①② | C.③ | D.②③ |
已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2,若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )
A.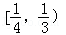 | B.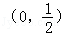 |
C.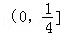 | D.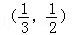 |
已知函数 ,
, ,设函数
,设函数 ,且函数
,且函数 的零点均在区间
的零点均在区间 内,则
内,则 的最小值为( )
的最小值为( )
| A.11 | B.10 | C.9 | D.8 |
若 为实数,
为实数, 表示不超过
表示不超过 的最大整数,则函数
的最大整数,则函数 在
在 上为( )
上为( )
| A.奇函数 | B.偶函数 | C.增函数 | D.周期函数 |
已知周期函数 的定义域为
的定义域为 ,周期为2,且当
,周期为2,且当 时,
时, .若直线
.若直线 与曲线
与曲线 恰有2个交点,则实数
恰有2个交点,则实数 的所有可能取值构成的集合为( )
的所有可能取值构成的集合为( )
A. 或 或   | B. 或 或   |
C. 或 或   | D.   |
已知函数 则
则 的单调增区间是( )
的单调增区间是( )
A. | B. |
C. | D. |