题目内容
若a>0,b>0,且a+b=1,则ab+ 的最小值为( )
的最小值为( )
 的最小值为( )
的最小值为( )| A.2 | B.4 | C. | D.2 |
C
由已知利用基本不等式得ab的取值范围而后换元利用函数的单调性求解.
由a+b=1,a>0,b>0得
2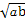 ≤a+b=1,∴
≤a+b=1,∴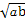 ≤
≤ ,∴ab≤
,∴ab≤ .
.
令ab=t,则0<t≤ ,
,
则ab+ =t+
=t+ ,结合函数的图象可知t+
,结合函数的图象可知t+ 在(0,
在(0, ]上单调递减,故当t=
]上单调递减,故当t= 时,t+
时,t+ 有最小值为
有最小值为 +4=
+4= .
.
由a+b=1,a>0,b>0得
2
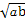 ≤a+b=1,∴
≤a+b=1,∴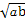 ≤
≤ ,∴ab≤
,∴ab≤ .
.令ab=t,则0<t≤
 ,
,则ab+
 =t+
=t+ ,结合函数的图象可知t+
,结合函数的图象可知t+ 在(0,
在(0, ]上单调递减,故当t=
]上单调递减,故当t= 时,t+
时,t+ 有最小值为
有最小值为 +4=
+4= .
.
练习册系列答案
相关题目
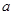 、
、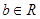 ,“
,“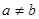 ”是“
”是“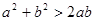 ”成立的( )
”成立的( )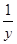 ,b=y+
,b=y+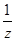 ,c=z+
,c=z+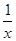 ,则a,b,c三数( )
,则a,b,c三数( )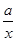 (x>0,a>0)在x=3时取得最小值,则a= .
(x>0,a>0)在x=3时取得最小值,则a= . ,
,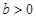 ,若
,若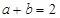 ,则
,则 的最小值为
的最小值为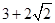
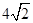
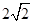
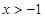 ,则函数
,则函数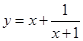 的最小值为( )
的最小值为( )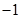
 的函数
的函数 的图象的两个端点为
的图象的两个端点为 ,
, 是
是 图象上任意一点,其中
图象上任意一点,其中 ,向量
,向量 ,若不等式
,若不等式 恒成立,则称函数
恒成立,则称函数 阶线性近似”. 若函数
阶线性近似”. 若函数 上“
上“



 的最小值为 。
的最小值为 。