题目内容
6．用四种不同的颜色给四棱锥P-ABCD的8条棱涂色，要求有公共点的两条棱的颜色不同，则不同的涂色方法有48种．分析 题意，四棱锥没有公共点的8条棱分4组，只有2种情况，利用排列知识，即可得出结论．
解答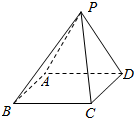 
解：由题意，四棱锥没有公共点的8条棱分4组，只有2种情况，（PA、DC；PB、AD；PC、AB；PD、BC）或（PA、BC；PD、AB；PC、AD；PB、DC），
那么不同涂法种数为2A44=48．
故答案为：48
点评 本题考查排列知识的运用，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
1．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈[0，2π））的图象如图所示，则φ的值为（ ）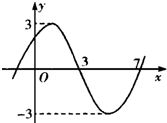
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{12}$ |
18．（重点中学做）函数f（x）=lnx+$\sqrt{\frac{x-3}{x-2}}$的定义域是（ ）
| A． | （0，2）∪[3，+∞） | B． | （-∞，2）∪[3，+∞） | C． | （2，3] | D． | [3，+∞） |
15．已知函数g（x）=sinx+acosx+2017满足g（x）+g（$\frac{7π}{3}$-x）=4034，又f（x）=asinx+cosx对任意x恒有f（x）≤|f（x0）|，则满足条件的x0可以是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{5π}{6}$ | D． | 以上选项均不对 |