Question

【题目】已知数列{an}满足a1＝1，且4an+1﹣anan+1+2an＝9（n∈N*）．

（1）求a2，a3，a4；

（2）由（1）猜想{an}的通项公式an ；

（3）用数学归纳法证明（2）的结果．

Answer 1

【答案】（1）（2）猜想：

（3）见解析

【解析】

（1）由a1＝1，且4an+1﹣anan+1+2an＝9即可求得a2，a3，a4的值，从而可猜想{an}的通项公式；

（2）由（1）猜得an，

（3）利用数学归纳法证明，分三步：①当n＝1时，猜想成立；②设当n＝k（k∈N*）时，猜想成立，去证明n＝k+1时猜想也成立（应用上归纳假设），③综上所述，即可证得猜想成立．

解：（1）由4an+1﹣anan+1+2an＝9得an+12，

∵a1＝1，

∴a2＝2﹣（），

同理可求，a3，a4，

（2）猜想：

（3）证明：①当n＝1时，猜想成立．

②设当n＝k（k∈N*）时，猜想成立，即ak，

则当n＝k+1时，有ak+1＝22，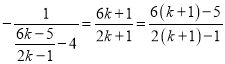

所以当n＝k+1时猜想也成立．

综合①②，猜想对任何n∈N*都成立．