题目内容
(本小题满分12分)函数f(x)=loga(x2-4ax+3a2), 0<a<1, 当x∈[a+2,a+3]时,恒有|f(x)|≤1,试确定a的取值范围.
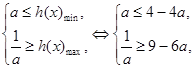
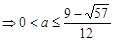 .
.本题考查对数型复合函数,求其定义域时要注意底数大于0且不等式于1,第二问考查了利用复合函数的单调性转化为不等式求参数,有一定难度.
求函数f(x)的定义域,依据对数函数的定义,底数大于0且不等于1,真数大于0,转化为不等式用参数a表示出函数f(x)的定义域;由这个结论知[a+2,a+3]必为(0,a)或者(3a,+∞)的子集,故[a+2,a+3]必为f(x)的单调区间,欲满足|f(x)|≤1,只须|f(a+2)|≤1,|f(a+3)|≤1同时成立,解此二不等式即可求得a的取值范围.
解:f(x)=loga(x2-4ax+3a2)= loga(x-3a)(x-a)
∵|f(x)|≤1恒成立,
∴ -1≤loga(x-3a)(x-a)≤1 ………………2分
∵ 0<a<1.
∴a≤(x-3a)(x-a)≤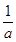 对x∈[a+2,a+3]恒成立. ………………5分
对x∈[a+2,a+3]恒成立. ………………5分
令h(x)= (x-3a)(x-a),
其对称轴x=2a. 又 2a<2, 2<a+2,
∴当x∈[a+2,a+3]时,
h(x)min=h(a+2),h(x)max=h(a+3). ……………8分
∴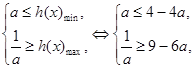
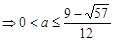 . ………………12分
. ………………12分
求函数f(x)的定义域,依据对数函数的定义,底数大于0且不等于1,真数大于0,转化为不等式用参数a表示出函数f(x)的定义域;由这个结论知[a+2,a+3]必为(0,a)或者(3a,+∞)的子集,故[a+2,a+3]必为f(x)的单调区间,欲满足|f(x)|≤1,只须|f(a+2)|≤1,|f(a+3)|≤1同时成立,解此二不等式即可求得a的取值范围.
解:f(x)=loga(x2-4ax+3a2)= loga(x-3a)(x-a)
∵|f(x)|≤1恒成立,
∴ -1≤loga(x-3a)(x-a)≤1 ………………2分
∵ 0<a<1.
∴a≤(x-3a)(x-a)≤
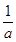 对x∈[a+2,a+3]恒成立. ………………5分
对x∈[a+2,a+3]恒成立. ………………5分令h(x)= (x-3a)(x-a),
其对称轴x=2a. 又 2a<2, 2<a+2,
∴当x∈[a+2,a+3]时,
h(x)min=h(a+2),h(x)max=h(a+3). ……………8分
∴
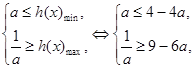
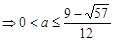 . ………………12分
. ………………12分
练习册系列答案
相关题目
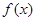 对于任意
对于任意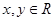 , 总有
, 总有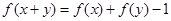 ,
,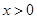 ,
,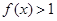
 上的单调递增函数
上的单调递增函数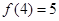 ,求解不等式
,求解不等式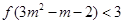
 的定义域为
的定义域为 ,且在
,且在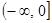 上是增函数.
上是增函数.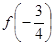 与
与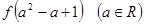 的大小;
的大小; ,求不等式
,求不等式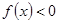 的解集.
的解集. 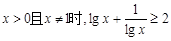
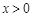 ,
,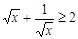
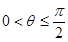 ,
,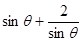 的最小值为
的最小值为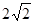
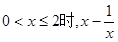 无最大值
无最大值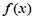 在
在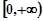 上为增函数,若不等式
上为增函数,若不等式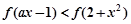 恒成立,则实数
恒成立,则实数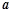 的取值范围为( )
的取值范围为( )
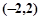
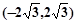

 有负根,则a的取值范围是_______________
有负根,则a的取值范围是_______________ 上的偶函数
上的偶函数 在
在 上是增函数,且
上是增函数,且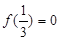 ,则不等式
,则不等式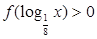 的解集是 ( )
的解集是 ( )



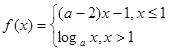 ,若
,若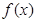 在
在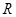 上单调递增,则实数
上单调递增,则实数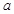 的取值范围为为
的取值范围为为
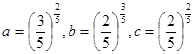 则a,b,c的大小关系是( ).
则a,b,c的大小关系是( ).