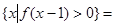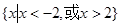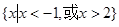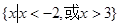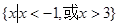题目内容
(本小题满分12分)
已知偶函数 的定义域为
的定义域为 ,且在
,且在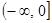 上是增函数.
上是增函数.
(Ⅰ)试比较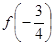 与
与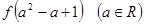 的大小;
的大小;
(Ⅱ)若 ,求不等式
,求不等式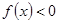 的解集.
的解集.
已知偶函数
 的定义域为
的定义域为 ,且在
,且在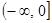 上是增函数.
上是增函数.(Ⅰ)试比较
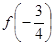 与
与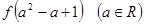 的大小;
的大小;(Ⅱ)若
 ,求不等式
,求不等式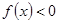 的解集.
的解集. :⑴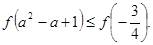 ;⑵不等式
;⑵不等式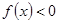 的解集为
的解集为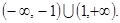
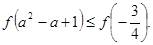 ;⑵不等式
;⑵不等式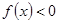 的解集为
的解集为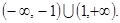
本试题主要考查了偶函数与单调性以及不等式的综合运用。
(1)先分析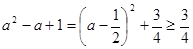 ,说明而偶函数
,说明而偶函数 在
在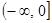 上是增函数
上是增函数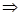
 在
在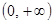 上是减函数.
上是减函数.
然后利用变量的不等关系得到结论。
(2)∵ 为偶函数,且
为偶函数,且 ,
,
∴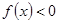
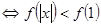 ,等价于
,等价于
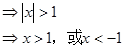 成立,得到范围。
成立,得到范围。
解:⑴∵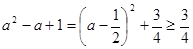 ,
,
而偶函数 在
在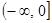 上是增函数
上是增函数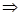
 在
在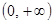 上是减函数.
上是减函数.
∴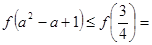
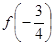 ,即
,即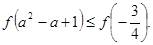
⑵∵ 为偶函数,且
为偶函数,且 ,
,
∴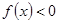
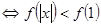
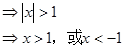
即不等式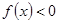 的解集为
的解集为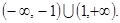
(1)先分析
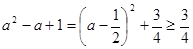 ,说明而偶函数
,说明而偶函数 在
在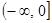 上是增函数
上是增函数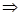
 在
在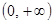 上是减函数.
上是减函数.然后利用变量的不等关系得到结论。
(2)∵
 为偶函数,且
为偶函数,且 ,
,∴
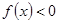
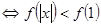 ,等价于
,等价于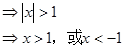 成立,得到范围。
成立,得到范围。解:⑴∵
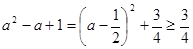 ,
,而偶函数
 在
在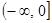 上是增函数
上是增函数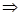
 在
在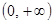 上是减函数.
上是减函数.∴
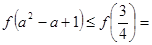
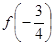 ,即
,即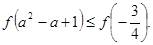
⑵∵
 为偶函数,且
为偶函数,且 ,
,∴
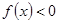
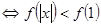
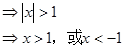
即不等式
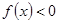 的解集为
的解集为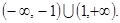

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
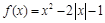 .(1)将函数
.(1)将函数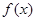 的解析式写成分段函数;
的解析式写成分段函数;
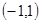 上的函数
上的函数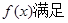
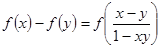 ;当
;当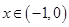 时,
时,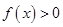 ,若
,若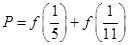 ,
,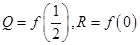 ,则P,Q,R的大小关系为( )
,则P,Q,R的大小关系为( )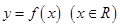 满足
满足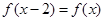 ,且
,且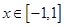 时,
时,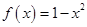
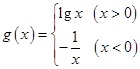 ,则函数
,则函数 在区间
在区间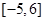 内的零点的个数为
内的零点的个数为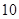
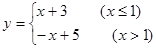 的最大值是
的最大值是 
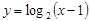
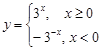
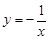
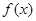 满足
满足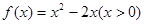 ,则
,则