题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() (
(![]() ).
).
(Ⅰ)证明数列![]() 为等差数列,并求
为等差数列,并求![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 满足
满足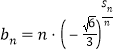 ,且
,且![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)证明见解析,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)通过对(n+1)an+1﹣(n+2)an=2变形、裂项可知![]() ﹣
﹣![]() =2(
=2(![]() ﹣
﹣![]() ),进而利用累加法、并项相加,计算即得结论;
),进而利用累加法、并项相加,计算即得结论;
(Ⅱ)通过(I)可知bn=n![]() ,通过令f(x)=x
,通过令f(x)=x![]() ,求导可知函数f(x)先增后减,进而计算可得结论.
,求导可知函数f(x)先增后减,进而计算可得结论.
∵(n+1)an+1﹣(n+2)an=2,
∴![]() ﹣
﹣![]() =
=![]() =2(
=2(![]() ﹣
﹣![]() ),
),
又∵![]() =1,
=1,
∴当n≥2时,![]() =
=![]() +(
+(![]() ﹣
﹣![]() )+(
)+(![]() ﹣
﹣![]() )+…+(
)+…+(![]() ﹣
﹣![]() )
)
=1+2(![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ﹣
﹣![]() )
)
=![]() ,
,
又∵![]() =1满足上式,
=1满足上式,
∴![]() =
=![]() ,即an=2n,
,即an=2n,
∴数列{an}是首项、公差均为2的等差数列;
(Ⅱ)解:由(I)可知![]() =
=![]() =n+1,
=n+1,
∴bn=n![]() =n
=n![]() ,
,
令f(x)=x![]() ,则f′(x)=
,则f′(x)=![]() +x
+x![]() ln
ln![]() ,
,
令f′(x)=0,即1+xln![]() =0,解得:x0≈4.95,
=0,解得:x0≈4.95,
则f(x)在(0, x0)上单调递增,在(x0,+![]() 单调递减.
单调递减.
∴0<f(x)≤max{f(4),f(5),f(6)},
又∵b5=5![]() =
=![]() ,b4=4
,b4=4![]() =﹣
=﹣![]() ,b6=6
,b6=6![]() =﹣
=﹣![]() ,
,
∴M的最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目