题目内容
已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE= ,O为AB的中点.
,O为AB的中点.
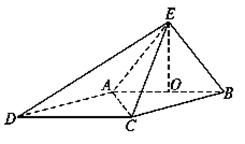
(Ⅰ)求证:EO⊥平面ABCD;
(Ⅱ)求点D到平面AEC的距离.
 ,O为AB的中点.
,O为AB的中点.
(Ⅰ)求证:EO⊥平面ABCD;
(Ⅱ)求点D到平面AEC的距离.
(Ⅰ)详见解析; (Ⅱ) 点D到平面AEC的距离为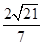 .
.
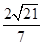 .
.试题分析:(Ⅰ)求证EO⊥平面ABCD,只需证明
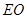 垂直平面
垂直平面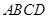 内的两条直线即可,注意到
内的两条直线即可,注意到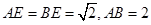 ,则
,则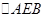 为等腰直角三角形,
为等腰直角三角形,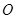 是
是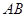 的中点,从而得
的中点,从而得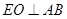 ,由已知可知
,由已知可知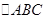 为边长为2的等边三角形,可连接CO,利用勾股定理,证明EO⊥CO,利用线面垂直的判定,可得EO⊥平面ABCD;(Ⅱ)求点D到平面AEC的距离,求点到平面的距离方法有两种,一.垂面法,二.等体积法,此题的体积容易求,且
为边长为2的等边三角形,可连接CO,利用勾股定理,证明EO⊥CO,利用线面垂直的判定,可得EO⊥平面ABCD;(Ⅱ)求点D到平面AEC的距离,求点到平面的距离方法有两种,一.垂面法,二.等体积法,此题的体积容易求,且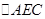 的面积也不难求出,因此可利用等体积,即
的面积也不难求出,因此可利用等体积,即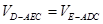 ,从而可求点D到面AEC的距离.
,从而可求点D到面AEC的距离.试题解析:(Ⅰ)连接CO.
∵
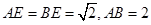 ,∴△AEB为等腰直角三角形. 1分
,∴△AEB为等腰直角三角形. 1分∵O为AB的中点,∴EO⊥AB,EO=1. 2分
又∵四边形ABCD是菱形,∠ABC=60°,
∴△ACB是等边三角形,
∴CO=
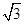 . 3分
. 3分又EC=2,∴EC2=EO2+CO2,∴EO⊥CO. 4分
又CO?平面ABCD,EO
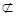 平面ABCD,∴EO⊥平面ABCD. 6分
平面ABCD,∴EO⊥平面ABCD. 6分(Ⅱ)设点D到平面AEC的距离为h.
∵AE=
 ,AC=EC=2,∴S△AEC=
,AC=EC=2,∴S△AEC=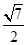 . 8分
. 8分∵S△ADC=
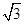 ,E到平面ACB的距离EO=1,VD-AEC=VE-ADC, 9分
,E到平面ACB的距离EO=1,VD-AEC=VE-ADC, 9分∴S△AEC·h=S△ADC·EO,∴h=
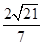 , 11分
, 11分∴点D到平面AEC的距离为
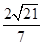 . 12分
. 12分
练习册系列答案
相关题目
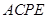 中,
中,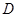 为
为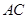 中点,
中点,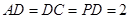 ,
,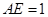 ,且
,且 ,现沿
,现沿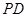 折起使
折起使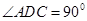 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.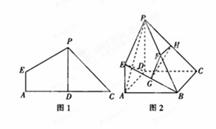
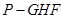 的体积;
的体积;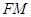 与直线
与直线 所成角为
所成角为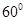 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由. 中, D是 AC的中点。
中, D是 AC的中点。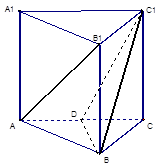
 //平面
//平面
 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
,

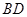 ⊥平面
⊥平面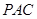 ;
;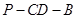 的大小;
的大小; 到平面
到平面 的距离.
的距离.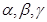 是三个不同的平面,上述命题中真命题的是
是三个不同的平面,上述命题中真命题的是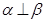 ,
,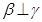 ,则
,则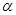 ∥
∥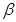 ;
;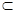
 ,
,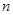 是两条不同直线,
是两条不同直线, ,
, 是两个不同平面,则下列命题错误的是( )
是两个不同平面,则下列命题错误的是( )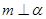 ,
,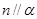 ,则
,则
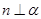 ,
, ,则
,则
 ,则
,则
 ,则
,则
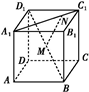
 A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 .
A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 .