题目内容
（本小题满分13分）
已知函数
（1）当
时，求曲线
处的切线方程；
（2）设
的两个极值点，
的一个零点，且
证明：存在实数
按照某种顺序排列后构成等差数列，并求
．
（1）y="x" - 2
（2）
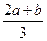
解析
练习册系列答案
能考试全能100分系列答案
相关题目
能考试全能100分系列答案题目内容
（本小题满分13分）
已知函数
（1）当时，求曲线处的切线方程；
（2）设的两个极值点，的一个零点，且证明：存在实数按照某种顺序排列后构成等差数列，并求．
（1）y="x" - 2
（2）
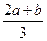
解析
能考试全能100分系列答案
都满足不等式
的所有函数
组成的集合记为M，例如，函数
。
，证明：
；
，并说明理由；
．
在点
处与直线
相切，求
的值；
的单调区
间与极值点．
是同时满足下列两个性质的函数
组成的集合：
，使得
．
是否属于集合
，求实数
的取值范围．
是定义域为R上的奇函数。
的值.
上的最小值为—2，求m的值。
,求:
;(2)
;(3)函数
.
=
.
上的单调性并加以证明.
的定义域为集合A，
；
，求
的值；
，
，求
及
的导函数
，
，
、
为实数。
，
）处切线的斜率为12，求
，求函数