题目内容
已知定点A(-1,0),F(2,0),定直线l:x=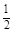 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由
【答案】
解:(1)设P(x,y),则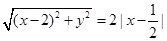
化简得x2-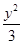 =1(y≠0)…………………………………………4分
=1(y≠0)…………………………………………4分
(2)①当直线BC与x轴不垂直时,设BC的方程为y=k(x-2)(k≠0)
与双曲线x2-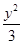 =1联立消去y得
=1联立消去y得
(3-k)2x2+4k2x-(4k2+3)=0
由题意知3-k2≠0且△>0
设B(x1,y1),C(x2,y2),
则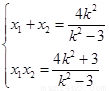
y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]
=k2(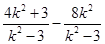 +4)
+4)
=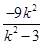
因为x1、x2≠-1
所以直线AB的方程为y=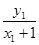 (x+1)
(x+1)
因此M点的坐标为(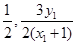 )
)
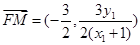 ,同理可得
,同理可得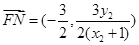
因此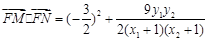
=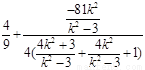
=0
②当直线BC与x轴垂直时,起方程为x=2,则B(2,3),C(2,-3)
AB的方程为y=x+1,因此M点的坐标为(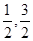 ),
),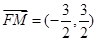
同理可得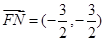
因此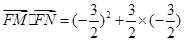 =0
=0
综上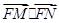 =0,即FM⊥FN
=0,即FM⊥FN
故以线段MN为直径的圆经过点F
【解析】略

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
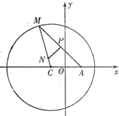 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足