题目内容
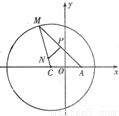
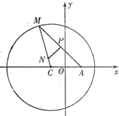 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足| AM |
| AP |
| NP |
| AM |
分析:由
= 2
,得P 为AM的中点,由
•
= 0,得NP⊥AM,故 NP为线段AM的中垂线,可得
NM+NC=2
(半径),点N的轨迹是以A、C为焦点的椭圆,从而求得点N的轨迹方程.
| AM |
| AP |
| NP |
| AM |
NM+NC=2
| 2 |
解答:解:C(-1,0),∵
= 2
,∴P 为AM的中点.∵
•
= 0,∴NP⊥AM.
故 NP为线段AM的中垂线,∴NM=NA.∵NM+NC=2
(半径),∴NA+NC=2
>AC=2,
根据椭圆的定义可得,点N的轨迹是以A、C为焦点的椭圆,a=
,c=1,∴b=1.
则点N的轨迹方程是
+y2=1,
故答案为:
+y2=1.
| AM |
| AP |
| NP |
| AM |
故 NP为线段AM的中垂线,∴NM=NA.∵NM+NC=2
| 2 |
| 2 |
根据椭圆的定义可得,点N的轨迹是以A、C为焦点的椭圆,a=
| 2 |
则点N的轨迹方程是
| x2 |
| 2 |
故答案为:
| x2 |
| 2 |
点评:本题考查轨迹方程的求法,椭圆的定义,判断点N的轨迹是以A、C为焦点的椭圆,是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
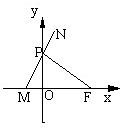 如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|.
如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|.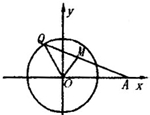 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.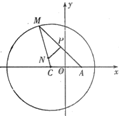 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足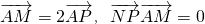 ,则点N的轨迹方程是________.
,则点N的轨迹方程是________. ,则点N的轨迹方程是 .
,则点N的轨迹方程是 .