题目内容
已知定点A(1,0),定直线l:x=5,动点M(x,y)
(Ⅰ)若M到点A的距离与M到直线l的距离之比为
,试求M的轨迹曲线C
1的方程.
(Ⅱ)若曲线C
2是以C
1的焦点为顶点,且以C
1的顶点为焦点,试求曲线C
2的方程.
分析:(Ⅰ)设d是点M到直线l:x=5的距离,由题意得:
=,由此能求出M的轨迹曲线C
1的方程.
(Ⅱ)由题意可知曲线C
2是双曲线,设方程为
-=1因为椭圆
+=1的顶点是(
(±,0),焦点是(±1,0)所以双曲线的顶点是(±1,0),焦点是
(±,0),由此能求出曲线C
2的方程.
解答:(本小题满分13分)
解:(Ⅰ)设d是点M到直线l:x=5的距离,由题意得:
=将上式两边平方,并化简,得
x2+y2=4即M的轨迹曲线C
1的方程是椭圆:
+=1.
(Ⅱ)由题意可知曲线C
2是双曲线,设方程为
-=1因为椭圆
+=1的顶点是(
(±,0),焦点是(±1,0)
所以双曲线的顶点是(±1,0),焦点是
(±,0)于是a=1,
c=所以 b
2=c
2-a
2=5-1=4
所以曲线C
2的方程是
x2-=1 点评:本题考查曲线方程的求法,具体涉及到椭圆和双曲线的简单性质,点到直线的距离公式,直线和圆锥曲线的位置关系.解题时要认真审题,仔细解答.
练习册系列答案
相关题目

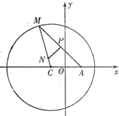 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足