题目内容
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.

(1)求证:CF∥平面AB1E;
(2)求三棱锥C-AB1E在底面AB1E上的高.

(1)求证:CF∥平面AB1E;
(2)求三棱锥C-AB1E在底面AB1E上的高.
(1)见解析(2)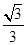
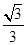
(1)证明:取AB1的中点G,连接EG,FG,
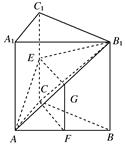
∵F、G分别是AB、AB1的中点,
∴FG∥BB1,FG=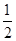 BB1.
BB1.
∵E为侧棱CC1的中点,
∴FG∥EC,FG=EC,
∴四边形FGEC是平行四边形,
∴CF∥EG,∵CF?平面AB1E,EG?平面AB1E,
∴CF∥平面AB1E.
(2)∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,
∴BB1⊥平面ABC.
又AC?平面ABC,∴AC⊥BB1,∵∠ACB=90°,∴AC⊥BC,
∵BB1∩BC=B,∴AC⊥平面EB1C,∴AC⊥CB1,
∴VA-EB1C=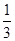 S△EB1C·AC
S△EB1C·AC
=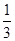 ×
×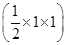 ×1=
×1=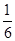 .
.
∵AE=EB1=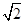 ,AB1=
,AB1=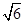 ,∴S△AB1E=
,∴S△AB1E=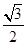 ,
,
∵VC-AB1E=VA-EB1C,∴三棱锥C-AB1E在底面AB1E上的高为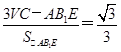 .
.

∵F、G分别是AB、AB1的中点,
∴FG∥BB1,FG=
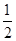 BB1.
BB1.∵E为侧棱CC1的中点,
∴FG∥EC,FG=EC,
∴四边形FGEC是平行四边形,
∴CF∥EG,∵CF?平面AB1E,EG?平面AB1E,
∴CF∥平面AB1E.
(2)∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,
∴BB1⊥平面ABC.
又AC?平面ABC,∴AC⊥BB1,∵∠ACB=90°,∴AC⊥BC,
∵BB1∩BC=B,∴AC⊥平面EB1C,∴AC⊥CB1,
∴VA-EB1C=
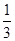 S△EB1C·AC
S△EB1C·AC=
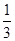 ×
×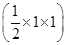 ×1=
×1=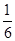 .
.∵AE=EB1=
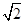 ,AB1=
,AB1=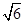 ,∴S△AB1E=
,∴S△AB1E=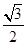 ,
,∵VC-AB1E=VA-EB1C,∴三棱锥C-AB1E在底面AB1E上的高为
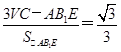 .
.
练习册系列答案
相关题目
 a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.

 .
.
 与平面
与平面 所成角的正弦值;
所成角的正弦值;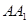 上是否存在点
上是否存在点 ?使得二面角
?使得二面角 的大小为60°,若存在,求出
的大小为60°,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. ⇒m⊥α;②
⇒m⊥α;② ⇒α⊥β;
⇒α⊥β; ⇒m∥n;④
⇒m∥n;④ ⇒m∥n
⇒m∥n