题目内容
如图所示,在矩形ABCD中,AB=a,BC= a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.

(1)求证:PA⊥CD;
(2)求直线PC与平面ACD所成角的正切值.
 a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
(1)求证:PA⊥CD;
(2)求直线PC与平面ACD所成角的正切值.
(1)详见解析,(2) .
.
 .
.试题分析:(1)折叠问题,首先要明确折叠前后量的变化,尤其是垂直条件的变化,本题要证明线线垂直,首先找线面垂直,因为关于
 垂直条件较多,所以考虑证明
垂直条件较多,所以考虑证明
 面
面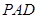 ,折叠前后都有条件
,折叠前后都有条件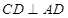 ,而折叠后
,而折叠后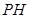
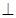 面
面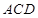 ,因此可由线面垂直得到
,因此可由线面垂直得到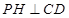 ,这样就可由线面垂直判定定理证到
,这样就可由线面垂直判定定理证到
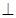 面
面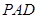 ,(2)求线面角,关键作出面的垂线.本题简单,因为
,(2)求线面角,关键作出面的垂线.本题简单,因为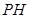
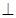 面
面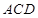 ,所以直线PC与平面ACD所成角就为
,所以直线PC与平面ACD所成角就为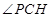 ,下面只需在直角三角形中解出
,下面只需在直角三角形中解出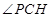 的正切值就可.
的正切值就可.试题解析:(1) 证明: 由题设,
 平面ACD,
平面ACD, 平面PAD
平面PAD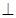 平面ACD, 3分
平面ACD, 3分交线为AD,又CD
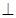 AD,
AD, CD
CD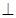 平面PAD,PA
平面PAD,PA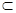 平面PAD,
平面PAD, CD
CD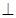 PA 6分
PA 6分(2)连接CH,则
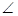 PCH为直线PC与平面ACD所成的角。
PCH为直线PC与平面ACD所成的角。作HG
 AC,垂足为G,连接PG,则AC
AC,垂足为G,连接PG,则AC 平面PHG
平面PHG  AC
AC PG, 9分
PG, 9分又在矩形ABCD中,AB=a,BC=
 a,
a,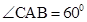
在直角
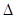 PGA中,PA=a,
PGA中,PA=a,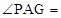
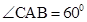
 AG=
AG=
在直角
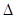 HAG中,AH=
HAG中,AH=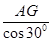 =
= ,又AC="2a," 2分
,又AC="2a," 2分在直角
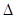 CAH中,根据余弦定理可得,CH=
CAH中,根据余弦定理可得,CH= ,
,在直角
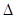 PHA中可得PH=
PHA中可得PH=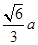 ,
, tan
tan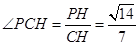 13分
13分
练习册系列答案
相关题目
 BC.
BC.

 ,直线
,直线 ,且有
,且有 ,则下列四个命题正确的个数为( )
,则下列四个命题正确的个数为( ) ∥
∥ 则
则 ;②若
;②若 ∥
∥ 则
则 则
则 ;
;



